|
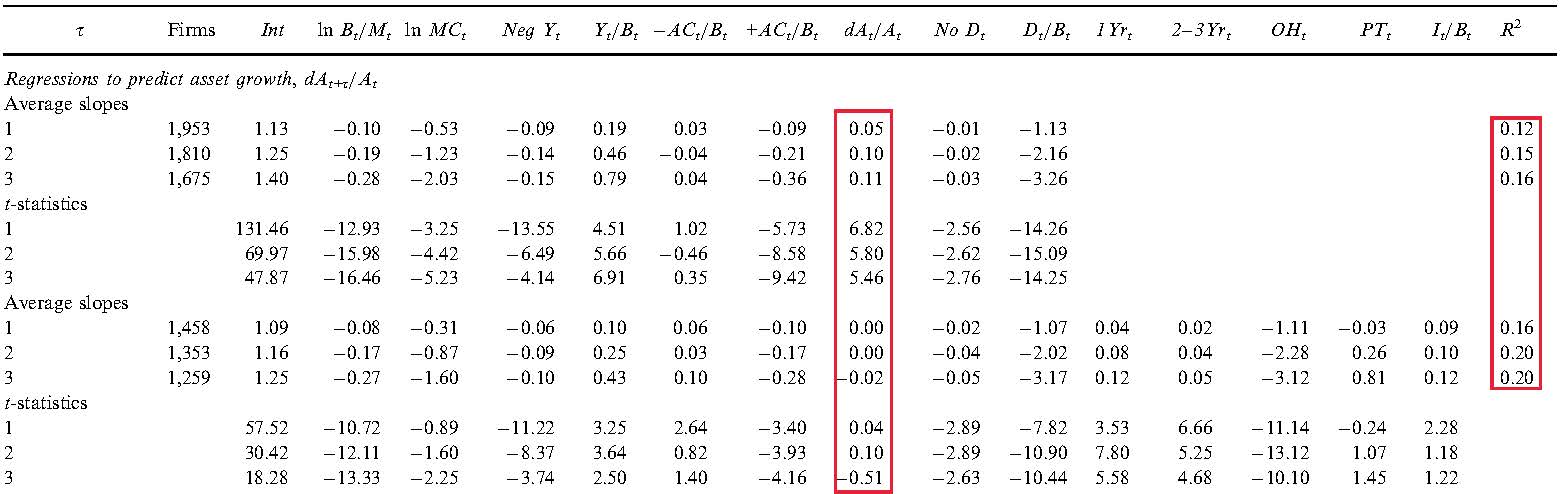
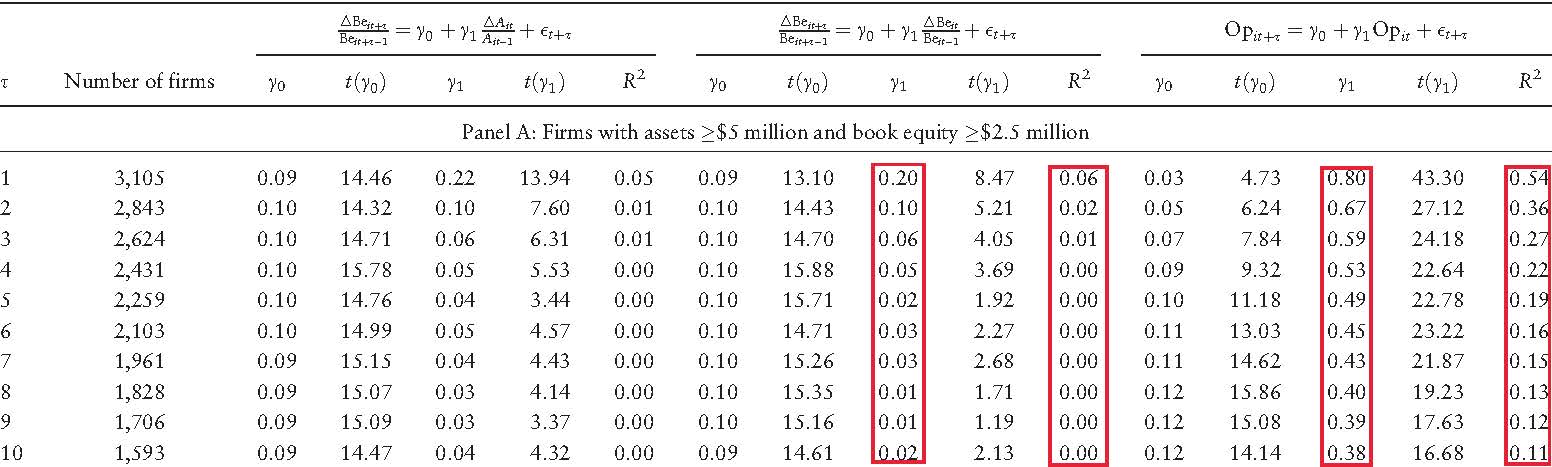
(An earlier, shorter version of this article appeared earlier today on alphaarchitect.com under the title “Investment, Expected Investment, and Expected Stock Returns”. I thank Wes Gray for soliciting the article.) A new DFA article by Rizova and Saito (2019) titled “Investment and Expected Stock Returns” rehashes old (in my view, largely discredited) arguments by Fama and French (2006, 2015) on the investment factor: i) Valuation theory predicts that expected investment is negatively correlated with expected return, all else equal; and ii) Current asset growth is a good proxy for expected investment. According to Fama and French, the negative relation between expected investment and expected return then gives rise to the investment factor, which captures the negative relation between current investment and expected return in the data. Based on Hou et al. (2019a), this blog shows that Fama and French’s arguments are fundamentally flawed. I also summarize the conceptual foundation of Hou, Xue, and Zhang's (2015) investment factor, a foundation which in my view better captures the underlying economics of the investment factor. A Positive Relation between Expected Investment and Expected Return in Valuation Theory In Fama and French’s formulation of valuation theory, the discount rate is the internal rate of return, which is constant over time. While a useful concept, the constant discount rate return clearly contradicts the well accepted notion of time-varying expected returns. For instance, it is nowadays well accepted that expected returns are most likely higher in recessions than in booms. Expected momentum profits are reliably positive but only within one year post-formation and are negative afterward. Hou et al. (2019a) reformulate valuation theory with one-period-ahead expected return. They show that the relation between expected investment and the one-period-ahead expected return is more likely to be positive in the reformulated valuation theory. See their paper for the detailed derivations. Empirically, Fama and French (2006) in fact report a positive, albeit weak, relation between expected investment and expected return. They write: “Contrary to the predictions of the valuation equation (3), however, the return regressions of Table 3 produce positive average slopes on the Table 2 regression proxies for expected asset growth, but they are not reliably different from zero (p. 507).” Specifically, in their Table 3, which is reproduced below, the highlighted column below is the slopes on expected investment in monthly cross-sectional return regressions. The slopes are mostly positive, albeit insignificant. The evidence says that expected investment estimated via their specifications is positively related to the expected return, although the relation is weak. Table 3 in Fama and French (2006): Monthly cross-sectional return regressions Current Asset Growth Is a Poor Proxy for Expected Investment Continuing on the (in my view, wrong) path of a negative relation between expected investment and expected return, Fama and French (2015) ditch the two specifications of expected investment in Table 2 of their 2006 article and switch to current asset growth as the proxy for expected investment. Doing so yields a desired negative relation between expected investment and expected return. However, current asset growth is all but a poor proxy for expected investment. The evidence is borne out in Table 2 in Fama and French (2006) reproduced below. The table shows annual cross-sectional regressions of future asset growth on lagged firm variables, one of which is current asset growth. If asset growth is a perfect proxy for expected asset growth, the slopes on current asset growth should be close to one and drive out all other variables. However, the first highlighted column below does not support this view. In the shorter specification, the slopes on asset growth are economically small, albeit significant, indicating only weakly positive autocorrelations of asset growth. In the longer specification, the slopes on asset growth are all virtually zero and insignificant. Table 2 in Fama and French (2006): Multiple regressions to predict asset growth Further evidence is provided in Table VII in Hou et al. (2019a) reproduced below. The table shows annual cross-sectional regressions of book equity growth on current asset growth and, separately, on current book equity growth. The first highlighted column shows that the slopes on current investment when predicting future investment are far from one, 0.2 in the first year, and quickly falls toward zero afterward. The R-square starts at 6% in year one and falls largely to zero afterward. Table VII in Hou et al. (2019a): Annual cross-sectional regressions of future book equity growth and future operating profitability The last five columns in the table above show the cross-sectional regressions of operating profitability on current operating profitability. Operating profitability is substantially more persistent than investment, the slope in the first year is 0.8, and the R-square 0.54. This evidence supports Fama and French’s (2015) use of operating profitability as expected operating profitability in their 5- and 6-factor models as well as Hou, Xue, and Zhang’s (2015) use of current return on equity (Roe) as expected Roe in the q-factor model. In particular, earnings are often characterized as a random walk in the accounting literature. In sum, the evidence is clear that current asset growth is a poor proxy for expected asset growth, but current operating profitability is a good proxy for expected operating profitability. The evidence refutes Fama and French’s (2015) arguments of the investment factor via the expected investment channel. Investment, Expected Investment, and Expected Stock Returns: The Investment CAPM Perspective In the investment CAPM (Zhang 2017), investment and expected investment are related to expected return in two opposite ways. Hou, Xue, and Zhang (2015) propose the investment factor as a key driving force of expected stock returns. In Corporate Finance, the net present value (NPV) of a project is its present value (discounted value of the project’s future cash flows) minus its investment costs today. The NPV rule says that a manager should invest in a given project, if and only if the present value of the project is greater than or equal to its investment costs. When initially facing many projects with nonnegative NPVs, the manager should start with the project with the highest NPV and work her way down the supply curve of projects. A good project has a low discount rate, high profitability, and low investment costs. As the manager takes more and more projects, their investment costs become higher and higher, and their profitability lower and lower. For the last project that the manager takes, its NPV should equal zero: (A) Investment costs = Present value = Profitability/Discount rate. The investment CAPM turns the NPV rule, which is a fundamental principle in Corporate Finance, on its head and transforms it into an Asset Pricing theory. Rewriting the NPV rule yields: (B) Discount rate = Profitability/Investment costs. Relative to profitability, high investment firms incur higher investment costs, meaning that their discount rates and expected returns must be low. Relative to investment, high profitability firms must have high discount rates and high expected returns. In all, investment and profitability are two key driving forces of expected stock returns. The investment factor arises naturally from equation (B). Intuitively, given profitability, high costs of capital (discount rates) imply low NPVs of new projects and low investments, and low costs of capital imply high NPVs of new projects and high investments. Equations (A) and (B) apply to a static model with only one period. In a multiperiod, dynamic model, equation (A) becomes: (A’) Investment costs = Present value = (Profitability + Present value of cash flows from next period onward)/Discount rate. However, with optimal investment, the present value of cash flows from next period onward equals expected investment costs next period (marginal q equals marginal costs of investment). Accordingly, equation (B) becomes: (B’) Discount rate = (Profitability + Expected investment costs)/Investment costs. Intuitively, if investment and expected investment costs are high next period, the present value of cash flows from next period onward must be high. Because the benefits to investment this period are primarily the present value from next period onward, the benefits to investment this period must also be high. As such, if expected investment costs are high next period relative to investment costs this period, or equivalently, if expected investment is high next period relative to current investment, the discount rate must be high. The discount rate must be high to offset the high benefits of investment this period to keep current investment low. This intuition behind the positive relation between expected investment (growth) and expected return is analogous to the intuition behind the positive relation between profitability and expected return, i.e., the Roe factor in the q-factor model. And this is the core intuition underlying the expected investment growth factor in the q^5 model of Hou et al. (2019b). Factor Spanning Tests: The q-factor model versus the Fama-French (2018) 6-factor model The following table updates Hou et al.'s (2019a) factor spanning tests. The tests show that the q-factor model cleanly subsumes the Fama-French 6-factor model in head-to-head contests. Specifically, in the 1967-2018 monthly sample, the investment and return on equity (Roe) factors in the q-factor model earn on average 0.38% and 0.55% per month (t = 4.59 and 5.44), respectively. Their alphas in the Fama-French 6-factor regressions are 0.1% and 0.27%, both of which are significant (t = 2.82 and 4.32), respectively. The Gibbons, Ross, and Shanken (GRS, 1989) test strongly rejects the null hypothesis that the Fama-French 6-factor model can subsume the investment and Roe factors. In all, despite having two more factors, the Fama-French 6-factor model cannot subsume the q-factor model in the data.
Conversely, HML, CMA, RMW, and UMD in the Fama-French 6-factor model earn on average 0.32%, 0.3%, 0.28%, and 0.64% per month (t = 2.42, 3.29, 2.76, and 3.73), respectively. More important, their alphas in the q-factor regressions are economically small (tiny in many cases) and statistically insignificant: 0.05%, 0.00%, 0.03%, and 0.14% (t = 0.49, 0.08, 0.32, and 0.61), respectively. The GRS test cannot reject the null hypothesis that the q-factor model can subsume the HML, CMA, RMW, and UMD factors. In all, despite having two fewer factors, the q-factor model fully subsumes the Fama-French 6-factor model, including UMD. Summary Fama and French’s (2006, 2015) arguments for the investment factor are fundamentally flawed. Valuation theory, once reformulated in terms of the one-period-ahead expected return, implies a positive relation between expected investment and expected return, a prediction which Fama and French’s (2006) evidence also indicates. In addition, unlike profitability, firm-level asset growth is not (that) persistent, meaning that current asset growth is a poor proxy for expected investment. Most tellingly, Fama and French (2018) seem to have abandoned any theoretical discipline when adding the momentum factor, UMD, into their 6-factor specification: "We include momentum factors (somewhat reluctantly) now to satisfy insistent popular demand. We worry, however, that opening the game to factors that seem empirically robust but lack theoretical motivation has a destructive downside: the end of discipline that produces parsimonious models and the beginning of a dark age of data dredging that produces a long list of factors with little hope of sifting through them in a statistically reliable way (p. 237, my emphasis)." In contrast, the investment factor arises naturally from the investment CAPM, which in essence is a restatement of the Net Present Value rule in Corporate Finance. Intuitively, given profitability, high costs of capital (discount rates) imply low NPVs of new projects and low investments, and low costs of capital imply high NPVs of new projects and high investments. In all, it is perhaps time to embrace the supply approach to asset pricing to distill some theoretical discipline that the field of empirical asset pricing has been sorely lacking since, well, Fama and French (1993). After all, empirically, factor spanning tests show that the q-factor model fully subsumes the Fama-French 6-factor model in head-to-head contests. References Fama, Eugene F., and Kenneth R. French, 1993, Common risk factors in the returns on stocks and bonds, Journal of Financial Economics 33, 3–56. Fama, Eugene F., and Kenneth R. French, 2006, Profitability, investment and average returns, Journal of Financial Economics 82, 491-518. Fama, Eugene F., and Kenneth R. French, 2015, A five-factor asset pricing model, Journal of Financial Economics 116, 1-22. Fama, Eugene F., and Kenneth R. French, 2018, Choosing factors, Journal of Financial Economics 128, 234-252. Gibbons, Michael R., Stephen A. Ross, and Jay Shanken, 1989, A test of the efficiency of a given portfolio, Econometrica 57, 1121–1152. Hou, Kewei, Haitao Mo, Chen Xue, and Lu Zhang, 2019a, Which factors? Review of Finance 23, 1-35. Hou, Kewei, Haitao Mo, Chen Xue, and Lu Zhang, 2019b, q^5, working paper, The Ohio State University. Hou, Kewei, Chen Xue, and Lu Zhang, 2015, Digesting anomalies: An investment approach, Review of Financial Studies 28, 650-705. Rizova, Savina, and Namiko Saito, 2019, Investment and expected stock returns, Dimensional Fund Advisors. Zhang, Lu, 2017, The investment CAPM, European Financial Management 23, 545-603.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
Lu Zhang
An aspiring process metaphysician Archives
September 2025
Categories |


 RSS Feed
RSS Feed