Lu's Blog

Parameter Instability

5/23/2020

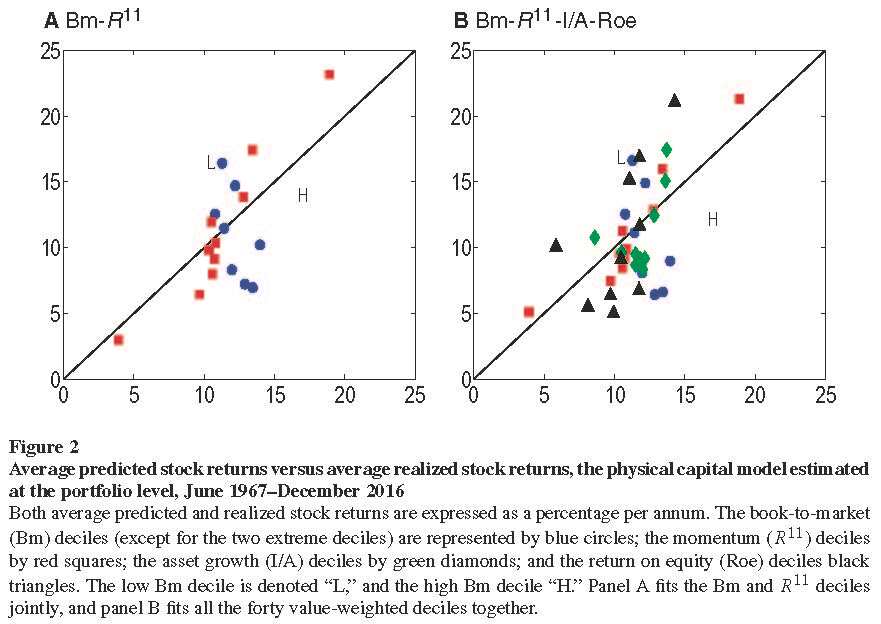
Our article titled “Aggregation, capital heterogeneity, and the investment CAPM” (Goncalves, Xue, and Zhang 2020) has just appeared in the June 2020 issue of Review of Financial Studies. A free copy is here as well as the internet appendix.

A recurring critique of my structural estimation line of work started in Liu, Whited, and Zhang (2009) is that the parameter estimates appear unstable across different testing portfolios. This fair and important critique has guided our effort in the past five years. Thank you for arguing with me.

Figure 2 from our latest publication replicates this difficulty. The parameter instability manifests itself as the failure of the baseline investment model in explaining value and momentum simultaneously (Panel A). The baseline model fits momentum but gets value upside down. Not surprisingly, the joint estimation failure persists once we add asset growth and return on equity deciles (Panel B).

Figure 3 shows that the joint estimation difficulty has largely been resolved within an extended two-capital model with working capital and fixed, physical capital. Our article also offers a range of improvements in terms of measurement and econometric specifications. Perhaps the most important improvement is to calculate the "fundamental" (model implied) stock return at the firm level before aggregating it to the portfolio level to match with the portfolio-level stock return.

Many important questions remain open. The measurement is all based on historical-cost accounting. Curious to see what happens with current-cost economic measurement. What about employment data? International data? Is it possible to develop ex-ante expected return measures out of this economic model that can compete with the prestigious and immensely important literature on implied costs of capital in accounting? Not sure, but I am eager to find out...

5 Comments

Umberto Sagliaschi

8/31/2020 11:58:00 am

I read with great interest your academic work, and I do agree on the underlying philosophy. The "anything goes" theorem is too often ignored, despite we all (investors) have experience of different tastes for risk and return. However, I have few questions/comments about your framework.

1) Firms have no market power. Holding the cost of capital constant, higher profitability (i.e. higher EbiTDA/Sales) may be the outcome instead of a substantial pricing power, especially for non-durable good producers where the Coase conjecture does not certainly apply. So higher profitability, holding investment/assets constant, may be related to a more rigid demand schedule. I made some algebra to check the consistency of my argument and would be just happy to share it with you (maybe is wrong, need to double check).

2a) If I understand correctly, you model debt as risk-free, with debt's rollover always possible under the NPG condition, and allow for the cost of debt to differ across firms. Since debt is risk-free, the cost of debt can be only higher and by means of some transaction cost added to the coupon rate. Looking at the first order condition, E(M(R^{ba})=1, it must be the case that the tax shield term just offsets the transaction cost charged on top of the coupon rate, which is equal to the risk-free rate as debt is always repaid in full. If this interpretation is correct, the firm's WACC is always equal to the firm's unlevered cost of capital, as the value of debt tax shield is fully offset by that of the implicit transaction costs that make the after tax cost of debt equal to the risk-free rate. If my interpretation is correct, I don't see how it is possible in your model to have a substantial heterogeneity in the before-tax cost of debt (at least within same country/currency firms).

2b) What about default, bankruptcy costs and agency costs? Wouldn't it be interesting to extend the investment CAPM using the no-commitment framework of DeMarzo and He (20209?

3) Working capital. I appreciated enormously the inclusion of working capital in the model, which is often an important investment component. Yet, your approach is a bit too much neoclassical to me, despite I am also a big fan of the neoclassical approach. First, if we deal with non-durable/non-storable goods, thinking about working capital~inventories is not immediate. However, the point is another one. Working capital, whether in the form of Inventories or Payables/Receivables, is driven by the firm's operating cycle, which is often "taken as given". Put differently, you can't change the payment days required by your suppliers, unless you are some sort of industry monopsonist. Why not including working capital then in a more reduced form, such as a fixed working capital / sales ratio? I think your model would be a) more realistic b) more tractable if to use it for an assessment of the "fundamental cost of capital".

4) Last comment. In one of your paper I read a statement like "firms do a good job in aligning their investment policies with the cost of capital". True, with a caveat though. Many CFOs, and there are surveys confirming this, use DCF/EVA/WACC models to take relevant investment decisions. However, all surveys available show that managers use either the CAPM to estimate the cost of equity or hurdle rates. A better alternative, at least in my opinion, could be reverse engineering a DCF, but it does not matter. If CFOs "learn" their cost of capital using the CAPM, and estimating beta historically, how much this "learning" component is likely to affect the investment CAPM?

Apologies for the long writing, looking forward to have your feedback.

Best,
Umberto

Lu Zhang

8/31/2020 11:04:11 pm

Thank you for your thoughtful comments. I've provided point-to-point responses in what follows.

On 1), I encourage you to write up your paper, which I am happy to read and comment on once available. The main challenges that I face are: (i) to demonstrate the empirical power of q-factors in the presence of competing factor models; and (ii) to establish that the investment CAPM is theoretically as fundamental as the consumption CAPM (but empirically more tractable). Both are tough challenges that have been exhausting my research time in the past decade.

You’re right in that most specifications in my work so far have featured constant returns to scale. With constant returns, I can write down Euler equations to take directly to the data. In quantitative theories, I work with decreasing returns to yield a well-defined cross-sectional distribution of firms. With Apple, Telsa, Amazon, etc., going through the roof right now, it’s natural to ask what happens with increasing returns, intangibles, and market power. It would be really cool to derive an expected return equation with these ingredients incorporated and then quantify their impact on asset prices in the real data. A major theoretical innovation is called for.

On 2a), I agree the cost of debt piece needs more work. At one point, I’ve attempted to embed a trade-off model of capital structure into the investment CAPM framework but couldn’t close the deal. I gave up after being lost in the math and couldn’t find my way back to the investment return = WACC equation. Any progress in this direction would be very useful. That said, I’ve probably tried too hard to be cute in insisting an analytical equation to take to the data. In general, there is nothing wrong with SMM if you have the stomach to wait for your code to converge.

I should probably point out that in my applications so far on cross-sectional equity returns, the related dispersion in cost of debt is small in magnitude. In addition, we measure costs of debt directly in the data, which are not risk-free. The Online Appendix of Goncalves, Xue, and Zhang (2020, RFS) contains some detailed evidence in this regard.

If you want to apply the investment CAPM to corporate bonds, a more careful modeling of capital structure would be very valuable.

On 2b), totally. As noted, my hands are completely full with the two aforementioned challenges. Please go ahead and work on these immensely interesting questions. Again, I’ll be happy to read and comment on your work after it’s ready to circulate.

One suggestion though. My work has been very applied and has become more so over the years. My questions are all empirically driven. And I strive to keep my model simple. You cannot specify a simpler model than the q-factor model without losing some of its important explanatory power. All I am trying to say is that I don’t see immediate benefits of default loss, agency costs, etc. in terms of helping explain anomalies. So, the economic questions will most likely arise from elsewhere.

For example, I am aware that almost all dynamic corporate models have risk neutrality. How would cross-sectionally expected returns change its basic conclusions quantitatively? Changing the pricing kernel from a constant beta to the Epstein-Zin one will get you started.

On 3), good point. I need to think a bit more about modeling working capital. The 2-capital model arises from, again, our wish to keep the model simple. A productive input without adjustment costs seems like the simplest way to go.

On 4), I am aware of the survey evidence that says CFOs use predominantly the CAPM in setting their costs of capital. However, our large-sample evidence does indicate a nice investment-expected return relation that conforms to the investment CAPM. Implicitly, what we are assuming is that CFOs have more information about their companies. And outside investors can learn about this (unobservable) information from (observable) corporate policies.

Thank you again for your questions and comments. I am very grateful.

9/1/2020 04:56:50 am

Thank you very much for your time and the very detailed clarifications.

I totally agree that from an empirical perspective, especially at portfolio level, your framework is sufficient to explain several interesting patterns of the cross of equity returns. Indeed, I was implicitly thinking about micro-applications, e.g. how can we use the firm's FOC to recover the cost of capital from appropriate measures of expected profitability. Here an example where I think some additional work needs to be done: a company with 40% pre-tax Return on Invested Capital and "average" Capex/Sales ratio (or, better, Capex/Invested Capital ratio), does not necessary have a double digit cost of equity or very high adjustment costs, as the higher RoIC may be driven by higher market power and therefore higher operating margins (e.g. Ferrari).

I'm working on some very preliminary notes of potential extensions of the model along this direction, mostly for my own academic interest. I will be very happy to get in touch once ready and have your very precious feedback.

In the meantime, many thanks again for your answers.

Umberto

9/1/2020 09:33:18 am

Certainly. I'll be happy to read and comment on your work. Thanks again for reaching out. Stay safe and healthy...

Ben French link

3/24/2021 11:18:25 pm

Totally unrelated, but do you think that practicioners should target I/A instead of value?

Your comment will be posted after it is approved.

Finance Colada

Parameter Instability

Leave a Reply.

Lu Zhang

Archives

Categories