|
I am happy to report that two of our recent publications have just made the highly cited lists in their respective journals: "Which Factors?" (Hou, Mo, Xue, and Zhang 2019) at the Review of Finance list and "Replicating Anomalies" (Hou, Xue, and Zhang 2020) at the Review of Financial Studies list. "Which Factors?": Article; Slides; and Presentation: "Replicating Anomalies": Article; Slides; and Presentation (repost from Vlog: Replicating Anomalies):
1 Comment
Take a look at the picture below. What animal do you see? Source: Rabbit–duck illusion Wikipedia Philosophers of science such as Kuhn (1962) and Feyerabend (1975) call the shift from duck to rabbit (and vice versa) as "gestalt switch." The drastic change of perspectives spells trouble for scientific progress. The crux is that competing research programs interpret the available facts in entirely different, incompatible ways based on their different yardsticks of scientific success (the incommensurability problem). The prior literature in asset pricing has largely perceived anomalies as indicating dysfunctional capital markets as a result of systematic investor mistakes and trading frictions (that prevent these mistakes from being eliminated). In contrast, my body of work has viewed anomalies as indicating well-functioning capital markets as a result of the net present value rule in capital budgeting on the part of managers. The change in perspective seems like a "gestalt switch." Back in the picture above, the animal cannot be a duck and a rabbit simultaneously. "Dubbit" doesn't exist. The real world is more ambiguous, though one can still ask the question which one of the two perspectives outlined above offers a more accurate description of capital markets in reality. Time will tell. The presentation below delves into the "gestalt switch" based on Liu, Whited, and Zhang (2009, Journal of Political Economy, "Investment-based Expected Stock Returns," see also article and slides): The latest word on GMMing investment returns is in Goncalves, Xue, and Zhang (2020, Review of Financial Studies, "Aggregation, Capital Heterogeneity, and the Investment CAPM," see article, slides, and the presentation below): Zhang (2005), titled "The Value Premium," is back in the news in academic circles. As flattered as I am with the latest attention, most of which I didn't exactly ask for, it occurs to me that I should check the Web of Science cites. While I do follow Google Scholar, which is only one click away, the last time I checked Web of Science was in December 2009, when I was putting a dossier together to come to Ohio State. Back in the late 1990s and early 2000s, after the publication of Fama and French (1993, 1996), one of the more pressing tasks facing asset pricing theorists is to explain the value premium. Many of their works in this wave of theorizing were published around 2005. With 15+ years of time test, the table below shows the scorecard based on citations (that are at least objective): I have put a recording together for "The Value Premium," in which I reflect on the methodological choices (largely implicit in this article) as well as open challenges in this theoretical literature. See below please as well as slides: In the next-to-last section of the presentation above, I share my take on the recent disappointing performance of the value premium in the data: First, the high-minus-low decile on book-to-market earns on average only 0.3% per month (t = 1.58) from January 1967 to December 2020. However, the high-minus-low decile on operating cash flow-to-market earns 0.8% (t = 4.18) in the same sample period. I view the evidence as saying that (i) book equity fails to capture intangibles per Lev's influential body of work. And (ii) the value of intangibles can still be ascertained, effectively, from cash flows (Penman 2009). Second, as in book-to-market, operating cash flow-to-market has also suffered from poor recent performance (though to a lesser degree). Barring from the Covid shock, the past decade has been the longest boom in history. The causal mechanism based on costly reversibility and countercyclical price of risk in Zhang (2005) would predict that the value premium should come back going forward. (The expected value premium is countercyclical.) To invoke Karl Popper, this prediction is highly falsifiable. Time will tell. Finally, please see below for a video presentation on "The CAPM Strikes Back? An Equilibrium Model with Disasters" (Bai, Hou, Kung, Li, and Zhang 2019) as well as slides. Among other things, this article extends Zhang's (2005) industry equilibrium to general equilibrium with heterogeneous firms. I have just put a recording together for the published version of "Replicating Anomalies" (Hou, Xue, and Zhang 2020, Review of Financial Studies). See below please as well as slides: Please also see below Jack Forehand and Justin Carbonneau's "Excess Returns" Podcast Episode 73 on our article: Nir Kaissar at Bloomberg wrote a cool article on "Amazon and Other Tech Giants Buck the Empire Trap." Nir's article draws the difference between our investment factor and our expected growth factor. Our factor series are available at our global-q data library. Because our expected growth factor is relatively new, I thought I could elaborate its intuition against the background of our investment factor. The investment CAPM (a reformulation of the Net Present Value rule in corporate finance) says that the discount rate equals the marginal benefit of investment divided by the marginal cost of investment. And the marginal benefit includes expected profitability and expected growth. The investment factor is built on tangible investment, which is measured as the growth rates of book assets on the balance sheet. Tangible investment has little impact on expected growth. And the investment CAPM implies a negative relation between tangible investment and the cost of capital (captured by our investment factor). However, the expected growth factor is (mostly) built on operating cash flow, which accounts for some of the most reliably measured intangible investment at the firm level, such as R&D. Intangible investment raises expected growth. And the investment CAPM implies a positive relation between intangible investment and the cost of capital (captured by our expected growth factor). These economic insights are explained in depth in the latest draft of our security analysis paper. The expected growth factor is from our 2021 RoF article. Please see Slides and the video presentation: We have just released the codes for the globally nonlinear projection algorithm developed in Petrosky-Nadeau and Zhang (2017) titled "Solving the Diamond-Mortensen-Pissarides Model Accurately" published at Quantitative Economics. Please see Codes as well as Article, Slides, and the video presentation: The codes for our 2018 article "Endogenous Disasters" at American Economic Review have already been released. Please see Codes as well as Article, Slides, and the video presentation: Happy Computing! I am honored to deliver my keynote on "Toward A Theory of Everything?" at the 6th Annual University of Connecticut Finance Conference this morning. The talk summarizes my scientific research program that aims to explain the equity premium puzzle in general equilibrium production economies, by integrating macro labor with asset pricing. Please see below for the video presentation, which might help with insomnia. While on the subject of vlog, I repost below my keynote on ”The Investment CAPM: Latest Developments” delivered at Swedish House of Finance Annual Conference on August 19, 2019. A wise man advises me that I should elaborate on the epistemological issues raised toward the end of my last post “Is Asset Pricing Scientific?” (April 3, 2021). This post is my response.
The Fama-French 3-factor model is arguably the most important work in asset pricing in the past 25 years. It is thus not surprising that the new way of thinking epitomized in the q-factor model has been met with high hurdles, one after another. To make sense of my professional predicament in the past decade, I have recently started to explore philosophy of science. Kuhn (1977, p. 357) describes five virtues that scientists must consider when deciding between an established theory and an upstart competitor. In particular, how should one choose between the Fama-French 3-, 4-, 5-, and 6-factor models on one side and the q-factor model and its extension, the q5 model, on the other? First, Kuhn says that a theory should be accurate: “within its domain, that is, consequences deducible from a theory should be in demonstrated agreement with the results of existing experiments and observations.” The head-to-head factor spanning tests reported in my last post clearly show that the q-factor model is more accurate than the 6-factor model. In fact, we have been reporting such evidence since 2014 (first with the 5- then with the 6-factor model). Second, Kuhn says that a theory should be consistent, “not only internally or with itself, but also with other currently accepted theories applicable to related aspects of nature.” The q-factor model is internally consistent. It is built from, and consistent with, the net present value rule in corporate finance. The rule says that, uncontroversially, investment policy is the first-order determinant of firm value. Riding on the first principle of firms, the q-factor model is also consistent with, and complementary to, the consumption CAPM. The investment versus consumption CAPM debate is only about the scope of applications, not a matter of theory replacement (like the q- versus 6-factor model). In my view, the 6-factor model falls short of the consistency criterion, both internal and external. Internally, it is not clear how UMD arises from valuation model. In addition, expected investment and expected return correlate positively in the model, not negatively (Hou et al. 2019). Externally, the theoretical linkage between common factors and ICAPM-APT state variables is tenuous (Zhang 2017). Third, a theory should have broad scope in that “a theory’s consequences should extend far beyond the particular observations, laws, or sub-theories it was initially designed to explain.” The q-factor model is broad. In particular, Hou, Xue, and Zhang (2015) write “the consumption model and the investment model of asset pricing are equivalent in general equilibrium, delivering identical expected returns. While the consumption model says that consumption risks are sufficient for accounting for expected returns, the investment model says that characteristics are sufficient. We take the latter prediction seriously and confront the q-factor model with a wide array of anomaly variables that are not directly related to investment and profitability (p. 658, footnote 8).” In other words, just like only beta matters in the CAPM, only investment and profitability matter for the cross-sectional expected-return dispersion in the q-factor model. In Popperian (1962) terms, this conjecture is very bold and highly refutable. Yet, the evidence largely confirms our conjecture. Popper would have liked the q-factor model. Fourth, a theory should be simple, “bring order to phenomena that in its absence would be individually isolated and, as a set, confused.” I started out with complicated modeling in Zhang (2005), simplified substantially to Euler equation tests in Liu, Whited, and Zhang (2009), and finally arrived at the investment and profitability factors in Hou, Xue, and Zhang (2015). It is simple to be complicated and complicated to be simple. Each layer of simplification comes with, I think, a deeper layer of understanding of the inner workings of capital markets. In the end, only the net present value rule is left standing. In philosophy of science, the no-miracles argument for scientific realism says that the predictive success of science would be a miracle if predictively successful scientific theories were not at least approximately true (Putnam 1975). In asset pricing, this argument implies that the strong explanatory power of the simple q-factor model would be a miracle if its underlying theory (the investment CAPM) was not at least approximately true in capital markets. Fifth, a theory should be fruitful of new research findings: “it should, that is, disclose new phenomena or previously unnoted relationships among those already known.” Lakatos (1970) defines a scientific research program as “progressive” as long as its theoretical growth keeps predicting novel facts with some success. A program is “degenerate” if its theoretical growth lags behind its empirical growth, that is, it gives only ex post, ad hoc explanations of facts anticipated by, and discovered in another program. If a research program progressively explains more than a rival, then it supersedes the rival. And the rival program can be eliminated. In Lakatosian terms, the q-factor model is one exemplar from a scientific research program that I call the supply theory of value. The “hard core” of this program is to price assets based on the first principles of their suppliers. To make contact with data in the real world, this hard core is supplemented with a variety of “protective belt.” The belt includes the measurement of investment, profitability, and expected growth as well as factor construction; specifications of marginal product of capital and adjustment costs as well as structural estimation via GMM; and specifications of the pricing kernel and productivity as well as quantitative investigation. I feel that this research program is “progressive” in that it has successfully addressed a wide range of important issues, including factor models, scientific explanations of asset pricing anomalies, linking factor premiums to fundamentals via structural estimation, and the equity premium puzzle, etc. I will leave it to the reader to decide where the Fama-French program of the 3-, 4-, 5-, and 6-factor models resides in the Lakatosian degenerate-progressive spectrum. Where I stand is an open secret. In short, evaluated with Kuhn’s five virtues (accuracy, consistency, scope, simplicity, and fruitfulness), I feel that the q-factor model is the rightful heir of the 3-factor model. The q-factor model inherits everything cool about the 3-factor model, especially its empirical methods, but fills its glaring lack of theoretical foundation. American Finance Association Code of Professional Conduct and Ethics (2016, 3 (a)) says: “Financial economists should work to provide an environment that encourages the free expression and exchange of scientific ideas. They should promote equal opportunity and treatment for all their colleagues, regardless of age, gender, race, ethnicity, national origin, religion, sexual orientation, disability, health condition, marital status, parental status, genetic information, or any other reason not related to scientific merit. More senior members of the profession have a special responsibility to facilitate the research, educational, and professional development of students and subordinates. This includes providing safe, supportive work environments, fair compensation and appropriate acknowledgement of their contribution to any research results (p. 1-2, my emphasis).” Alas, “ought” does not mean “is.” If “is” is already achieved, there is no need to set up “ought” to begin with. Whether a theory change from the 3-factor model to the q-factor model occurs, and if yes, how long it will take, are left for future historians, who, presumably, will try to reconstruct how academic finance really works. I no longer worry about such things. I enjoy my work. And that’s all that matters to me. References Hou, Kewei, Chen Xue, and Lu Zhang, 2015, Digesting anomalies: An investment approach, Review of Financial Studies 28 (3), 650-705. Hou, Kewei, Haitao Mo, Chen Xue, and Lu Zhang, 2019, Which factors? Review of Finance 23 (1), 1-35. Kuhn, Thomas S., 1977, Objectivity, value judgment, and theory choice, in T. S. Kuhn: The Essential Tension, University of Chicago Press. Lakatos, Imre, 1970, Falsification and the methodology of scientific research programmes, in I. Lakatos and A. Musgrave: Criticism and the Growth of Knowledge, Cambridge University Press. Liu, Laura Xiaolei, Toni M. Whited, and Lu Zhang, 2009, Investment-based expected stock returns, Journal of Political Economy 117 (6), 1105-1139. Popper, Karl R., 1962, Conjectures and Refutations: The Growth of Scientific Knowledge, Basic Books. Putnam, Hilary, 1975, What is mathematical truth? In H. Putnam: Mathematics, Matter and Method, Collected Papers Vol. 2. Cambridge University Press. Zhang, Lu, 2005, The value premium, Journal of Finance 60 (1), 67-103. Zhang, Lu, 2017, The investment CAPM, European Financial Management, 23 (4), 545-603. We have just released the latest q-factors data library that has been updated through December 2020. The table below shows that the Hou-Xue-Zhang (2015) q-factor model continues to fully subsume the Fama-French (2018) 6-factor model in the extended sample from January 1967 to December 2020. The 6-factor model cannot explain the q-factors. The investment premium is 0.33% per month (t = 4.1), with a 6-factor alpha of 0.09% (t = 2.55). The return on equity (Roe) premium is 0.51% (t = 4.96), with a 6-factor alpha of 0.25% (t = 4.09). The Gibbons-Ross-Shanken (1989, GRS) test strongly rejects the 6-factor model with the null hypothesis that the 6-factor alphas of the investment and Roe premiums are jointly zero (p = 0.00). More important, the Hou-Xue-Zhang q-factor model fully subsumes the Fama-French factors. The HML, CMA, and RMW premiums are on average 0.24%, 0.27%, and 0.27% per month (t = 1.76, 3.05, and 2.77), but their q-factor alphas are virtually zero, -0.01%, 0.01%, and 0.02% (t = -0.09, 0.39, and 0.3), respectively. UMD is on average 0.62% (t = 3.63), but its q-factor alpha is only 0.18% (t = 0.86). The GRS test fails to reject the q-factor model with the null that the q-factor alphas of HML, CMA, RMW, and UMD are jointly zero (p = 0.7). So, is asset pricing scientific? Popper's (1959) demarcation between science and non-science hinges on falsifiability. Lakatos (1970) says that a scientific research program should be "progressive" in that it needs to explain empirical puzzles with few ad hoc fixes. Despite his early "mob psychology" regarding theory choice in Structure (1962), Kuhn (1977) later characterizes a good theory in terms of its accuracy, consistency, scope, simplicity, and fruitfulness. Finally, Feyerabend (1975) argues that science is an anarchic enterprise with no particular epistemic order. While conscientious about external forces at work, I am determined to show Feyerabend is wrong about asset pricing. References Feyerabend, Paul, 1975, Against Method, New Left Books. Kuhn, Thomas S., 1962, The Structure of Scientific Revolutions, University of Chicago Press. Kuhn, Thomas S., 1977, Objectivity, value judgment, and theory choice, in T. S. Kuhn, The Essential Tension, University of Chicago Press. Lakatos, Imre, 1970, Falsification and the methodology of scientific research programmes, in Criticism and the Growth of Knowledge, I. Lakatos and A. Musgrave (eds.), Cambridge University Press. Popper, Karl, 1959, The Logic of Scientific Discovery, Hutchinson & Co. The article “Searching for the equity premium” (with Hang Bai) is now forthcoming at Journal of Financial Economics (paper, slides). For its motivation and overview of key results, please see my last blog posted on 10/18/2020. A surprising insight from our revision is the properties of investment and hiring returns. Despite a high average labor share in output calibrated to 74.6% (Gollin 2002), the capital share in the market equity is on average 92.6%! As such, even though labor market frictions play a central role in our search economy, the stock market is mostly for shareholders. Panel A below shows the scatter-plot of the capital share in value against aggregate productivity in our economy. As in a Covid map, dark red means high density, and light green low density. The value-weight of capital exhibits countercyclical dynamics, approaching 100% in very bad times, meaning that the shadow value of labor goes to zero. (In Panel B, the labor share in output is countercyclical, not surprisingly. Panel C shows an alternative labor share, in which wage equals the marginal product of labor, is weakly countercyclical, due to the CES production function.) The 92.6% estimate of the value-weight of capital has broad implications beyond this paper. In the cross section, the prior literature has mostly examined investment returns due to severe limitations of firm-level labor data. If we are right in that stock returns primarily consist of investment returns, prior cross-sectional results based on investment returns are likely to survive extensions to labor. Finally, I wish to acknowledge a weakness of the model (see Section 4.5). It turns out the postwar US sample is not representative at all from the model's perspective. In 10,000+ simulations, we could not find a single path with the equity premium no lower than, but the consumption volatility no higher than that in the postwar US sample. I suspect that a similar problem might also be present in the Rietz-Barro exogenous disaster literature, although I have not seen an explicit discussion yet. So the search continues... Hang Bai (UConn) and I have just circulated our new working paper titled “Searching for the equity premium” (paper, slides).
We view this work as a solid progress report toward the holy grail of macro-finance, which (in our view) is a unified theory of asset prices and business cycles. The persistence of the Mehra-Prescott (1985) equity premium puzzle in general equilibrium production economies has given rise to a long-standing dichotomy in macro-finance. Finance specifies “exotic” preferences and exogenous cash flow dynamics to match asset prices but ignore firms (Campbell and Cochrane 1999; Bansal and Yaron 2004; Barro 2006). Macroeconomics analyzes full-fledged dynamic stochastic general equilibrium (DSGE) models but ignore asset prices with primitive preferences (Christiano, Eichenbaum, and Evans 2005; Smets and Wouters 2007). This macro-finance dichotomy has left many important questions unanswered. What are the microfoundations underlying the exogenously specified, often complicated cash flow dynamics in finance models (Bansal, Kiku, and Yaron 2012; Nakamura, Steinsson, Barro, and Ursua 2013)? What are the essential ingredients in the production side that can endogenize the key elements of cash flow dynamics necessary to explain the equity premium? To what extent do time-varying risk premiums matter quantitatively for macroeconomic dynamics? How large is the welfare cost of business cycles in a general equilibrium production economy that replicates the equity premium? We embed the standard Diamond-Mortensen-Pissarides search model of equilibrium unemployment into a DSGE framework with recursive utility and capital accumulation. Highlights of our quantitative results include:
In all, the DSGE model with recursive utility, search frictions, and capital accumulation is a good start to forming a unified theory of asset prices and business cycles. Our article titled “Aggregation, capital heterogeneity, and the investment CAPM” (Goncalves, Xue, and Zhang 2020) has just appeared in the June 2020 issue of Review of Financial Studies. A free copy is here as well as the internet appendix. A recurring critique of my structural estimation line of work started in Liu, Whited, and Zhang (2009) is that the parameter estimates appear unstable across different testing portfolios. This fair and important critique has guided our effort in the past five years. Thank you for arguing with me. Figure 2 from our latest publication replicates this difficulty. The parameter instability manifests itself as the failure of the baseline investment model in explaining value and momentum simultaneously (Panel A). The baseline model fits momentum but gets value upside down. Not surprisingly, the joint estimation failure persists once we add asset growth and return on equity deciles (Panel B). Figure 3 shows that the joint estimation difficulty has largely been resolved within an extended two-capital model with working capital and fixed, physical capital. Our article also offers a range of improvements in terms of measurement and econometric specifications. Perhaps the most important improvement is to calculate the "fundamental" (model implied) stock return at the firm level before aggregating it to the portfolio level to match with the portfolio-level stock return. Many important questions remain open. The measurement is all based on historical-cost accounting. Curious to see what happens with current-cost economic measurement. What about employment data? International data? Is it possible to develop ex-ante expected return measures out of this economic model that can compete with the prestigious and immensely important literature on implied costs of capital in accounting? Not sure, but I am eager to find out... The q-factors library at global-q.org has just been updated through December 2019. The table below reports the latest head-to-head factor spanning tests: The Hou-Xue-Zhang (2015) q-factor model continues to dominate the Fama-French (2018) 6-factor model in the January 1967--December 2019 sample. On the one hand, the 6-factor model cannot subsume the q-factors. The investment premium is 0.36% per month (t = 4.45), with a 6-factor alpha of 0.09% (t = 2.65). The return on equity (Roe) premium is 0.54% (t = 5.46), with a 6-factor alpha of 0.26% (t = 4.25). The Gibbons-Ross-Shanken (1989, GRS) test strongly rejects the 6-factor model based on the null hypothesis that the 6-factor alphas of the investment and Roe premiums are jointly zero (p = 0.00). On the other hand, the q-factor model fully subsumes the Fama-French factors. The HML, CMA, and RMW premiums are on average 0.3%, 0.29%, and 0.28% per month (t = 2.29, 3.24, and 2.82), but their q-factor alphas are tiny, 0.04%, 0.01%, and 0.03% (t = 0.35, 0.23, and 0.35), respectively. The momentum factor, UMD, is on average 0.63% (t = 3.66), but its q-factor alpha is small, only 0.15% (t = 0.66). The GRS test fails to reject the q-factor model based on the null that the q-factor alphas of HML, CMA, RMW, and UMD are jointly zero (p = 0.79). Don't take my word for it. Go ahead and replicate the numbers. If your replication fails, I am the jerk. Otherwise, how about using the better factor model from now on? That's right. Ten years on, it seems that the q-factor model is indeed "A Better Factor Model That Explains More Anomalies." My apologies for taking so long, but please know that we're doing the best we can. Our working paper titled "An augmented q-factor model with expected growth" (with Kewei, Haitao, and Chen) is now forthcoming at Review of Finance. The paper is formerly titled "q5." Alas, who knew that the compiled output of the LaTeX source code "$q^5$" would be invisible to Google Scholar? Oh well, live and learn.
The expected growth factor, its 2 by 3 benchmark portfolios on size and expected growth, the expected growth deciles, and the 3 by 5 testing portfolios on size and expected growth are all available to download at global-q.org. We're waiting for Compustat to update its data in early February. Once the data become available, we will update and circulate the testing portfolios on all 150 anomalies examined in our q5 paper. Conceptually, in the investment CAPM, firms with high expected investment growth should earn higher expected returns than firms with low expected investment growth, holding current investment and profitability constant. Intuitively, if expected investment is high next period, the present value of cash flows from next period onward must be high. Consisting mainly of this present value, the benefit of current investment must also be high. As such, if expected investment is high next period relative to current investment, the current discount rate must be high to offset the high benefit of current investment to keep current investment low. Empirically, we estimate expected growth via cross-sectional forecasting regressions of investment-to-assets changes on current Tobin’s q, operating cash flows, and changes in return on equity. Independent 2 by 3 sorts on size and expected growth yield the expected growth factor, with an average premium of 0.84% per month (t = 10.27) and a q-factor alpha of 0.67% (t = 9.75). The t-values far exceed any multiple-testing adjustment that we are aware of. We augment the q-factor model (“q”) with the expected growth factor to form the model (“q5”). We then perform a large-scale horse race with other recently proposed factor models, including the Fama-French (2018) 6-factor model (“FF6”) and their alternative 6-factor model (“FF6c”), in which the operating profitability factor is replaced by a cash-based profitability factor, as well as several other factor models. As testing portfolios, we use the 150 anomalies that are significant (|t| ≥ 1.96) with NYSE breakpoints and value-weighted returns from January 1967 to December 2018 (Hou, Xue, and Zhang 2019). The large set includes 39, 15, 26, 40, and 27 across the momentum, value-versus-growth, investment, profitability, and intangibles categories. The q5 model is the best performing model. The figure below shows the fractions of significant alphas across all and different categories of anomalies. Across all 150, the q5 model leaves 15.3% significant, a fraction that is lower than 34.7%, 49.3%, and 39.3% across the q, FF6, and FF6c model, respectively. In terms of economic magnitude, across the 150 anomalies, the mean absolute high-minus-low alpha in the q5 model is 0.19% per month, which is lower than 0.28%, 0.3%, and 0.27% across the q, FF6, and FF6c model, respectively. The q5 model is also the best performer in each of the categories. In particular, in the momentum category, the fraction of significant alphas in the model is 10.3%, in contrast to 28.2%, 48.7%, and 35.9% across the q, FF6, and FF6c model, respectively. In the investment category, the fraction of significant alphas in the q5 model is 3.9%, in contrast to 34.6%, 38.5%, and 30.8% across the q, FF6, and FF6c model, respectively. While bringing expected growth to the front and center of empirical asset pricing, we acknowledge that the (unobservable) expected growth factor depends on our specification, and in particular, on operating cash flows as a predictor of future growth. While it is intuitive why cash flows are linked to expected growth, we emphasize a minimalistic interpretation of the q5 model as an effective tool for dimension reduction. The Fractions of Significant (|t| ≥ 1.96) Alphas Across Different Categories of Anomalies The paper titled "Unemployment Crises" (with Nicolas Petrosky-Nadeau) is now forthcoming at Journal of Monetary Economics. Our historical time series for U.S. unemployment rates and labor productivity (January 1890-December 2017) as well as vacancy rates (January 1919-December 2017) are available to download at this link. Nicolas and I have been as careful as we can when compiling the historical series, by building on the latest economic history literature. The following picture is the U.S. historical Beveridge curve. The convexity clearly indicates the congestion externality arising from matching frictions in the labor market. More important, the prewar observations, especially those from the Great Depression, make the Beveridge curve substantially flatter than it otherwise would have been. The 2007-2009 Great Recession is well aligned with the overall curve even without the Great Depression. Theoretically, we show that a search model of equilibrium unemployment, when calibrated to the mean and volatility of the postwar unemployment rates, implies empirically plausible persistence and unconditional probability of unemployment crises (states with the unemployment rates above 15%).
We also implement a Cole-Ohanion style accounting exercise for the Great Depression, but within the search framework. With a measured negative labor productivity shock that amounts to a magnitude of 3.4 unconditional standard deviations in the postwar sample, the model predicts a 35.8% drop in output from 1929 to 1933 and a high unemployment rate of 32.9% in June 1933. Both are empirically plausible. We also demonstrate the impact of detrending on the accounting exercise, a point that has not been emphasized in the prior literature. All in all, we suggest that a unified search model with the same parameters is a good start to understanding labor market dynamics in both the pre- and post-war samples simultaneously. (This blog post is the last of a 4-part sequence based on my working paper fresh from the oven: "q-factors and investment CAPM, which is a solicited, analytical essay on the big-picture of the investment CAPM. Due to its length, I am splitting it into 4 parts on my blog. The link above gives the complete pdf, which also provides detailed references.)
Challenges While many open questions remain in the investment CAPM literature, due to space limitations, I only discuss what I perceive as the two most important challenges in this essay. A Risky Mechanism of Momentum Momentum is a success story for the investment CAPM. Recall from January 1968 to December 2018, UMD earns on average 0.64% per month (t-value = 3.73). However, its q-factor alpha is only 0.14% (t-value = 0.61). The Roe factor does all the heavy lifting, as UMD has a large Roe-factor loading of 0.9 (t-value = 5.85), while its loadings on the other 3 factors are insignificant. In the structural estimation of Goncalves, Xue, and Zhang (2019), the investment CAPM explains value and momentum simultaneously, and the “tug of war” between current investment and expected investment plays a key role in the model’s performance. Nevertheless, a major gap in our knowledge exists. What exactly are the risks underlying momentum? To answer this question, one needs more than factor regressions and Euler equation tests. Only fully specified quantitative theories are up to the task. Recall Zhang (2005) has tied the value premium to business cycle risks. Alas, I am aware that momentum, and equivalently, the Roe factor premium are both significantly negative in that model. Also in partial equilibrium, Johnson (2002) ties momentum to expected growth and argues that expected growth is risky. Sagi and Seasholes (2004) argue that momentum winners have more growth options than momentum losers and that growth options are risky. An important, open question is how to combine Zhang’s value with Johnson’s and Sagi and Seasholes’ momentum mechanisms in a unified framework. A unified model imposes internal consistency that is vital for theories. Li (2018) is the only exception that makes sense to me. More work is sorely needed. Other Asset Classes An advantage of the consumption CAPM, and more generally, the SDF framework, is that it can in principle be applied to different asset classes simultaneously. In contrast, the investment CAPM has so far been mostly applied to equity pricing. However, I caution that the consumption side’s advantage of applying to different asset classes should not be taken too literally. After all, failures in explaining returns of different asset classes are definitely worse than failures in explaining just stock returns. Behavioral under- and overreaction apply to different asset classes (Asness, Moskowitz, and Pedersen, 2013). But sticking labels is no theory. More important, any asset has suppliers, which must face certain tradeoffs in making optimal supply decisions. It seems straightforward to apply the investment CAPM to global stocks, country equity indices, corporate bonds, and real estates. Other asset classes such as currencies, government bonds, and commodities require additional, creative theorizing. The challenge is to cleanly separate the supply-side tradeoff from the SDF. Because of aggregation, to me, SDF is the source of all ills in asset pricing and should be avoided at all costs. Conclusion I am ready to answer the fundamental questions raised at the beginning of this essay. What explains all the consumption CAPM anomalies? Well, the consumption CAPM anomalies are the investment CAPM regularities, all of which conform to the NPV rule in Corporate Finance. Capital markets obey standard economic principles. Anomalies in fact indicate well functioning, efficient capital markets. The world makes sense! The consumption CAPM fails so badly because of the well known aggregation problem (Kirman, 1992). The pain of aggregation is likely manageable for aggregate asset pricing (and for DSGE models, unless you want to study wealth inequality). However, the pain is insurmountable for the cross section, which is in essence a microeconomic problem. And our ubiquitous representative investor is out of depth. Despite its enormous, ever-lasting influence in practice, Graham and Dodd’s (1934) Security Analysis has yet to find its rightful home in finance theory. We’re blind to this parallel universe (otherwise known as practice) because of the consumption CAPM’s single-minded, dogmatic focus on demand. Graham and Dodd are squarely on supply. And the NPV rule is the first place one would go to put the 2 and 2 together. Characteristics-based factors are linear approximations to the nonlinear investment return equation in the investment CAPM. Characteristic factors are on as solid theoretical grounds in the investment CAPM as aggregate consumption growth in the consumption CAPM. Taking aggregation seriously, aggregate consumption growth is not even a factor. Neither are all other macroeconomic factors. Post-earnings-announcement drift persists for 50 years since Ball and Brown (1968) because it is part of expected returns, as predicted by the investment CAPM (the Roe factor). Why has there not been a coherent behavioral theory for 35 years since De Bondt and Thaler (1985)? Because such a theory likely doesn’t exist. If a full menu of psychological biases gives rise to underreaction, and another full menu to overreaction, we have an embarrassment of riches. A “theory” that explains everything (with no discipline) explains nothing. (This blog post is the third of a 4-part sequence based on my working paper fresh from the oven: "q-factors and investment CAPM, which is a solicited, analytical essay on the big-picture of the investment CAPM. Due to its length, I am splitting it into 4 parts on my blog. The link above gives the complete pdf, which also provides detailed references.)
Implications As a disruptive innovation, the investment CAPM thinks about asset pricing very differently from the consumption CAPM and behavioral finance, with broad-ranging implications for academic finance research and asset management practice. Complementarity with the Consumption CAPM In his magnum opus, Alfred Marshall (1890, Principles of Economics [1961, 9th edition, p. 348]) writes: “We might as reasonably dispute whether it is the upper or under blade of a pair of scissors that cuts a piece of paper, as whether value is governed by utility or costs of production. It is true that when one blade is held still, and the cutting is affected by moving the other, we may say with careless brevity that the cutting is done by the second; but the statement is not strictly accurate, and is to be excused only so long as it claims to be merely a popular and not a strictly scientific account of what happens.” Asset pricing theory is just value theory in microeconomics extended to uncertainty and over time. From this perspective, clearly, the consumption CAPM is conceptually incomplete. The crux is that it exclusively focuses on the demand of risky assets, while abstracting from the supply altogether. Alas, anomalies are primarily empirical relations between firm characteristics and expected returns. Without modeling firm characteristics, it is impossible to fully explain anomalies within the consumption CAPM. Even if an SDF specification is discovered that fits the consumption CAPM with anomaly portfolios, one still has to explain why the consumption betas would be aligned with investment-to-assets, Roe, book-to-market, momentum, and other anomaly variables. By focusing on the supply of risky assets, while abstracting from the demand altogether, the investment CAPM is the missing “blade” of equilibrium asset pricing, symmetrically and neatly complementing to the consumption “blade.” The investment CAPM and the consumption CAPM combine to form the pair of “scissors” of equilibrium pricing. The glorious achievements of the consumption CAPM are well known. I interpret its major contribution as time-varying expected returns, which largely resolve Shiller’s (1981) excess volatility puzzle in aggregate asset pricing. But why does the consumption CAPM fail so badly in explaining anomalies in the cross section? Zhang (2017) blames the intractable aggregation problem. Investors are heterogeneous in preferences, beliefs, and information sets, all of which make the demand-based pricing extremely difficult. The Sonnenschein-Mantel-Debrew theorem in equilibrium theory says that individual rationality imposes essentially no restrictions on aggregate demand, meaning that the aggregation problem over heterogeneous investors is largely intractable (Kirman, 1992). It is possible that for aggregate, macro-level asset pricing, a representative agent still suffices but fails for micro-level asset pricing in the cross section. Who’s the marginal investor for Apple Inc.? Anyone’s guess is as good as mine. Derived from the first principle of individual firms, the investment CAPM is relatively immune to the aggregation problem. Who’s the marginal supplier for Apple Inc. shares? Well, easy, that’s Apple Inc.. Tim Cook most likely has more impact on Apple Inc.’s market value via his operating, investing, and financing decisions than many Apple Inc. shareholders like me via portfolio decisions in their retirement accounts. The investment CAPM formalizes the linkage between corporate decisions and asset prices. The major contribution of the investment CAPM is cross-sectionally varying expected returns, which largely resolve anomalies in the cross section. In particular, the consumption CAPM anomalies are the investment CAPM regularities. Because of the inescapable aggregation difficulty facing the consumption CAPM and no such challenge facing the investment CAPM, EMH must be detached from the consumption CAPM and reattached to the investment CAPM. How many more decades of the consumption CAPM failures do we have to endure to let the lesson sink in that firm characteristics are not even modelled? The step going from an individual investor problem to a consumption-based SDF that prices all assets requires aggregation, which is all but automatic. Asset pricing is not all about SDF, which is only demand-based. The overreaching tendencies of the consumption CAPM, detrimental to our Science, must stop. You don’t see me pretending that the investment CAPM has anything to do with personal finance, household finance, or portfolio allocation. An EMH Counterrevolution to Behavioral Finance The anomalies literature is the empirical foundation of behavioral economics. The investment CAPM shows that the empirical foundation is all but an illusion. Start with: Realized returns = expected returns + abnormal returns. When an anomaly variable forecasts realized returns, there are tautologically two parallel interpretations. One, which is the behavioral view, says that the variable is forecasting abnormal returns. As such, pricing errors are predictable, violating EMH. The other, which is the EMH view, says that the anomaly variable is related to expected returns, but the pricing errors are unpredictable. The consumption CAPM and the investment CAPM are both expected-return models. Both are consistent with EMH. In the anomalies literature (and in asset management industry), the behavioral view is extremely popular. Behavioral finance has gained its prominence by documenting the CAPM alphas and sticking labels such as under- and over-reaction to them. While rejecting the CAPM is the more accurate interpretation of the evidence, the interpretation of rejecting EMH altogether certainly appears to be more impactful. More important, for a long time, the consumption CAPM is the only asset pricing theory in the land. Given the exclusive focus on investors, it’s not unreasonable to interpret the failure of the consumption CAPM as investor irrationality. The investment CAPM has changed the big picture in its entirety. I deal with Fama’s (1991) joint-hypothesis problem by replacing the consumption CAPM with the investment CAPM. With the suppliers of risky assets at the center of analysis, the anomalous evidence is largely consistent with the NPV rule in Corporate Finance. Remember EMH only says that pricing errors are not predictable. The investment CAPM alphas are mostly small and unpredictable. And the expectations of the investment CAPM are entirely rational. I separate EMH from investor rationality. Again, EMH only says that pricing errors are not predictable. It doesn’t say all investors are rational. A common counterargument against my EMH defense is that if investors set a firm’s equity price too high, its manager will just blindly adjust her investment decisions per her first-order condition. As a result, both the equity price and investment are wrong. This argument is specious at best. It ignores the powerful equilibrating role of the supply side. Some investors might be optimistic and attempt to bid up the equity price too high. But with a manager’s cool head, the supply of risky shares goes up, flooding cold water over the fire of irrational exuberance. The wrong price will drop toward the equilibrium price. In the special case of no adjustment costs, in particular, Tobin’s q will forever be one, regardless of how irrational investors are. This equilibrating role of the supply side seems to have been greatly underappreciated by academics and practitioners alike. I should concede that the complex equilibrating process between demand and supply is largely unknown. I have seen models of heterogeneous investors, and separately, models of heterogeneous firms. But I have yet to see a model with both heterogeneous investors and heterogeneous firms, likely because of its computational intractability. As such, all we can do is to use simpler models to gain insights. Behavioral finance relies on dysfunctional, inefficient markets for its mechanisms to work. With the investment CAPM, I view anomalies as regularities from the NPV rule in well functioning, efficient markets. As such, the argument that anomalies must necessarily imply investor irrationality is wrong. Anomalies most likely have less to do with investors and more to do with managers. The NPV rule is as fundamental an economic principle as diversification. Capital markets obey standard economic principles! However, because the complex equilibrating process between demand and supply is unknown, and perhaps even unknowable, I cannot say that the observed prices are completely deprived of wrong decisions from investors. However, remember the Sonnenschein-Mantel-Debrew theorem says that investor rationality and aggregate rationality are completely detached. Investors can be irrational, but the marginal (aggregate) investor might not, and vice versa. As such, the failures of the consumption CAPM might have nothing to say about EMH. Behavioral economists can hide behind this aggregation problem all they want and claim relevance. But it’s no coincidence that a coherent behavioral theory has yet to appear after 35 years since De Bondt and Thaler (1985). Given the time test, I feel that such a theory likely doesn’t even exist. While I contend that behavioral finance has almost nothing to say about equilibrium asset prices, I do think that it has a major role to play in areas like personal finance and household finance. Identifying and rectifying investor mistakes in these areas are enormously important for human welfare. However, these areas are partial equilibrium in nature. Without dealing with aggregation, these fields have limited implications for equilibrium asset prices. How I Defend Fama A watershed article is Fama and French (1992). It is this paper from the EMH inventor that abandons the CAPM, which is largely the only asset pricing theory at the time, thereby stimulating the development of behavioral finance. Although Fama and French (1993) quickly attempt to patch up the hole with their 3-factor model by adding SMB and HML into the CAPM, the floodgate has been opened. Fama (1998) tries to contain the resulting tsunami but to little avail. With a wrong hammer in their hands (as firm characteristics are all condensed into a Lucas tree), theorists have largely stood on the sidelines looking on, with precious little to say about the EMH versus behavioral finance debate. It is informative to compare Fama’s (1998) EMH defense 20 years ago with my current defense based on the investment CAPM. Fama makes 2 points. First, apparent overreaction is about as common as underreaction. As anomalies seem to split randomly between underreaction and overreaction, Fama claims that EMH wins. Second, anomalies are sensitive to changes in measurement. Anomalies with value-weighted returns are smaller than with equal-weighted returns. Also, calendar-time 3-factor regressions are more reliable than long-horizon event studies. Kothari (2001) echoes Fama in emphasizing the sensitivity of measurement and the need of coming up with a theory of inefficient markets as null hypotheses. Like his EMH insight, Fama’s empirics has no peers. As acknowledged in Zhang (2017), the empirical design of the q-factor model, including its factor construction, formation of testing portfolios, econometric tests, and most important, the taste of the economic question, are all deeply influenced by Fama and French (1993, 1996). I also take the value- versus equal-weight lesson to heart and give it a demonstration on steroids in Hou, Xue, and Zhang (2019). Alas, I do not find Fama’s (1998) chance argument persuasive. Anomalies do not just randomly split between under- and over-reaction camps. The two types of anomalies are systematically different. To a theorist, the systematic pattern is exciting, because it indicates hidden economic law(s) to be discovered. The hidden law turns out to be the investment CAPM (a restatement of the NPV rule in Corporate Finance), as demonstrated in Hou, Xue, and Zhang (2015). The “overreaction” anomalies are all just different manifestations of the investment factor, and the “underreaction” anomalies are all just different manifestations of the Roe factor. I do not find Fama and French’s (1993, 1996) interpretation of risk factors for SMB and HML persuasive either. To their credit, the lack of a risk interpretation for momentum has stopped them from adding it into their factor model until 2018 (Fama and French, 2018). It is statistically correct to view SMB, HML, and perhaps even UMD as risk factors from the intertemporal CAPM and/or APT. However, the interpretation is on shaky economic grounds because size, book-to-market, and prior short-term returns are never modeled in the two theoretical frameworks. As such, the risk interpretation seems like a mere assertion. This concern is why Hou, Xue, and Zhang (2015) interpret the q-factors only as common factors that summarize the cross-sectional variation of average stock returns. In particular, I find the concept of covariance superfluous. Yes, the consumption CAPM is all about covariance, but the investment CAPM is all about characteristics. If a characteristic is significant in cross-sectional regressions, its long-short factor is likely to earn a significant average return. And if a long-short factor earns a significant average return in the time series, its underlying characteristic is likely to be significant in cross-sectional regressions. As such, the q-factor model is simply a linear factor approximation to the nonlinear characteristics model of the investment CAPM. Going from a characteristic to a factor is mostly mechanical, and vice versa. In particular, stock returns of firms with similar investment-to-assets tend to comove together because their investment returns are similar as a result of similar investment-to-assets. Stock returns of firms with similar Roe and expected growth tend to comove together because their investment returns are also similar for analogous reasons. Comovement is nothing mysterious. More fundamentally, the investment CAPM advances a new perspective of “factors.” In the consumption CAPM, factor models are linear approximations of the intertemporal marginal rate of substitution for the representative investor. Aggregate variables such as the growth rate of industrial production, inflation rate, the default premium can be used to substitute out consumption, giving rise to the classic macroeconomic risk factor model of Chen, Roll, and Ross (1986). Because the consumption CAPM is in essence a macroeconomic model, factors are commonly perceived as aggregate, systematic sources of covariation. To the extent that size, book-to-market, and momentum are not modelled within the consumption CAPM, these factors have been (wrongfully, in my view) perceived as ad hoc, arising from “fishing” expeditions. In contrast, the investment CAPM offers a new, microeconomic perspective of “factors.” The comovement of stock returns among stocks with similar investment, profitability, and expected growth arises from the comovement of their similar investment returns. Characteristics-based factors are on as solid economic grounds in the supply theory of asset pricing as aggregate consumption growth in the demand theory of asset pricing. If one takes aggregation seriously, aggregate consumption growth is not even a factor. Neither are most other aggregate variables. Security Analysis within Efficient Markets Graham and Dodd (1934) define Security Analysis as “concerned with the intrinsic value of the security and more particularly with the discovery of discrepancies between the intrinsic value and the market price (p. 17).” Their philosophy is to invest in undervalued securities that are selling below the intrinsic value “justified by the facts, e.g., the assets, earnings, dividends, and definite prospects (p. 17).” Alas, the intrinsic value is not exactly identified. To protect against its estimation errors, Graham (1949) advocates the “margin of safety,” i.e., investors only purchase a security when its market price is sufficiently below its intrinsic value. EMH and Security Analysis have historically been viewed as diametrically opposite. On the one hand, the traditional view of academic finance, with the CAPM as its workhorse theory, dismisses security analysis as pure luck, likens security analysts to astrologers, and recommends investors to passively hold only the market portfolio. Bodie, Kane, and Marcus (2017) maintain: “[T]he efficient market hypothesis predicts that most fundamental analysis is doomed to failure (p. 356).” In a recent interview with Bloomberg on November 5, 2019, Fama even labels equity research on Wall Street as “business-related pornography.” On the other hand, honoring the 50th anniversary of Graham and Dodd (1934), Warren Buffett (1984) showcases 9 famous investors and argues that their successful performance is beyond chance. Buffett goes on to say: “Our Graham & Dodd investors, needless to say, do not discuss beta, the capital asset pricing model or covariance in returns among securities. These are not subjects of any interest to them. In fact, most of them would have difficulty defining those terms (p. 7).” Buffett then mocks finance academics as out of touch with the real world: “Ships will sail around the world but the Flat Earth Society will flourish (p. 15).” Wall Street practitioners, not surprisingly, are overwhelmingly sympathetic to the behavioral view, and believe EMH to be a relic of the past. An old joke helps illustrate the schism between academics and practitioners. An asset manager asks an academic: “If you are so smart, why aren’t you rich?” to which the academic replies: “If you are so rich, why aren’t you smart?” EMH is down in the dumps only because the consumption CAPM is a rundown dumpster truck. I have yet to meet an asset manager who even mentions the consumption CAPM, not even once, yet the consumption CAPM is virtually all we are allowed to talk about in academia (unless you’re a behavioral economist). The investment CAPM once again changes the big picture. Recall the investment CAPM says: Discount rate = (profitability + expected investment costs) / investment costs. In the denominator, investment costs equal Tobin’s q (marginal costs of investment equal marginal q). As such, the investment CAPM prescribes that to earn higher expected returns, investors should buy stocks with high quality (measured as high profitability and high expected growth) at bargain prices. This prescription is exactly what Graham and Dodd (1934) have been saying and what Wall Street asset managers have been practicing for 85 years. Finally, after such a long exile, Security Analysis has found its rightful home in finance theory. However, my treatment of Security Analysis differs from Graham and Dodd’s (1934) in a fundamental way. Writing way, way before the arrival of equilibrium theory, Graham and Dodd largely have a constant discount rate in mind as the expected-return model. Their remarkable business acumen enables them to intuit their way to the ever-lasting investment truth of buying high quality stocks at bargain prices. Their monumental work predates academic finance by at least 4 decades. Indeed, in at late as the 1970s, the random walk hypothesis (with a constant discount rate) is still the workhorse theory for EMH. In the 1980s and 1990s, the consumption CAPM rises up to meet Shiller’s (1981) excess volatility challenge and moves the needle from a constant discount rate to time-varying expected returns as the workhorse theory in EMH. With the investment CAPM, I am trying to move the needle once again to cross-sectionally varying expected returns. Shiller attributes all excess volatility to predictable pricing errors against EMH, but the consumption CAPM attributes it to time-varying expected returns within EMH. Analogously, Graham and Dodd (1934) attribute the performance of security analysis to predictable pricing errors against EMH, but the investment CAPM attributes it to cross-sectionally varying expected returns, all within EMH. Empirically, Hou, Mo, Xue, and Zhang (2019c) show that their model goes a long way toward explaining prominent security analysis strategies, including Frankel and Lee’s (1998) intrinsic-to-market value, Piotroski’s (2000) fundamental score, Greenblatt’s (2005) “magic formula,” Asness, Frazzini, and Pedersen’s (2019) quality-minus-junk, Buffett’s Berkshire, Bartram and Grinblatt’s (2018) agnostic analysis, as well as Penman and Zhu’s (2014, 2018) expected-return strategies. Also, Hou et al. show that the latest factor models cannot fully explain Buffett’s alpha and interpret the evidence as saying that discretionary, active management cannot be fully replaced by passive factor investing. Identifying sources of quality and quantifying their impact on expected returns leave plenty of room for active management. Rational Expectations Economics Make no mistake. The investment CAPM is the latest product from the Lucas-Sargent rational expectations economics. While I no longer believe that the end stage of economics is a Fortran program, the Lucas-Sargent teaching of microfoundation is deeply embodied in the investment CAPM. My Wharton theoretical training has given me a strong immune system against behavioral finance, despite being embedded in the hostile territory of the anomalies literature for 20 years. If I cannot write down an optimization-based model to explain a stylized fact, I don’t understand the fact. A “model” with no optimization is just sticking labels to the fact to be explained. True to the nature of the anomalies literature, with my Rochester empirical training, I have also given life to the investment CAPM with the careful, empirical measurement in the Fama-French tradition. While there are still a few mopping-up operations left to do, the anomalies literature, which used to be a major embarrassment for rational expectations economics, is no more. On the contrary, I have turned it into a triumph of rational expectations. My macroeconomist compatriots can go on refining the all-important DSGE models, without worrying about all the fires of capital markets, as the investment CAPM has put them out, mostly. I should clarify that my aggregation critique against the consumption CAPM applies to the specific context of anomalies in the cross section. For aggregate asset pricing, the consumption CAPM does well, although it remains to be seen to what extent aggregation would bite once the consumption CAPM is embedded into a full-fledged equilibrium model with production. Analogously, my aggregation critique does not apply, at least not directly, to the mainstream DSGE models in modern quantitative macroeconomics. (This blog post is the second of a 4-part sequence based on my working paper fresh from the oven: "q-factors and investment CAPM, which is a solicited, analytical essay on the big-picture of the investment CAPM. Due to its length, I am splitting it into 4 parts on my blog. The link above gives the complete pdf, which also provides detailed references.)
Methods The investment CAPM literature has taken its key predictions to the data via a variety of approaches, including factor regressions, structural estimation, and quantitative theories. Factor Models Hou, Xue, and Zhang (2015) propose and test the q-factor model, which implements the investment CAPM via the Fama-French (1993) portfolio approach. The q-factor model says that the expected return of an asset in excess of the riskfree rate is described by its sensitivities to the market factor, a size factor, an investment factor, and a return on equity (Roe) factor. The size, investment, and Roe factors are constructed from 2 by 3 by 3 sorts on market equity, investment-to-assets, and Roe. Empirically, the q-factor model goes a long way toward summarizing the cross section of average stock returns. The model explains many anomalies that bedevil the Fama-French 3-factor model, such as Jegadeesh and Titman’s (1993) momentum (Fama and French, 1996). Most anomalies are just different manifestations of investment and profitability. The data for the q-factors and testing portfolios are available for download at global-q.org. Intuition On the one hand, sorting on net stock issues, composite issuance, book-to-market and other valuation ratios, as well as long-term reversal is closer to sorting on investment than on profitability. As such, these diverse sorts reflect their common implied sort on investment. The flow-of-fund constraint of firms says that their uses of funds must equal their sources of funds. As such, all else equal, equity issuers should invest more and have lower costs of capital than nonissuers. In addition, firms use different capital goods in their operating activities, including working capital, physical property, plant, and equipment, and (measured) intangibles. As such, total asset growth is the most comprehensive measure of investment-to-assets, a simple measure that aggregates over investments in heterogeneous capital goods. The value factor is redundant in the presence of the investment factor. In the investment CAPM, investment increases with marginal q, which in turn equals average q with constant returns to scale. Average q and market-to-book equity are close cousins and are identical twins without debt. As such, value stocks with low valuation ratios should invest less and, all else equal, should earn higher expected returns than growth stocks with high valuation ratios. High valuation ratios come from a stream of positive shocks on fundamentals, and low valuation ratios a stream of negative shocks on fundamentals. Growth stocks typically have high long-term prior returns, and value stocks low long-term prior returns. As such, long-term reversal also reflects the investment factor. Firms with high long-term prior returns should invest more and have lower costs of capital than firms with low long-term prior returns. On the other hand, sorting on earnings surprises, short-term prior returns, and financial distress is closer to sorting on profitability than on investment. As such, these diverse sorts reflect their common implied sort on profitability. Intuitively, shocks to earnings are positively correlated with shocks to returns, contemporaneously. Firms with positive earnings shocks experience immediate stock price increases, and firms with negative earnings shocks experience immediate stock price drops. As such, momentum winners should have higher expected profitability and earn higher expected returns than momentum losers. In addition, less financially distressed firms have higher profitability and, all else equal, should earn higher expected returns than more financially distressed firms. As such, the distress anomaly is just another manifestation of the profitability factor. Subsequent Work The q-factor model has effectively ended the quarter-century reign of the Fama-French (1993) 3-factor model as the leading model in empirical asset pricing. During the long process, the q-factor model has stimulated a large subsequent literature on factor models. Fama and French (2015) attempt to fix their 3-factor model by incorporating their own versions of the investment and profitability factors to form a 5-factor model. Fama and French (2018) further add the momentum factor, UMD, to form their 6-factor model. However, Hou, Mo, Xue, and Zhang (2019a) show that the 4-factor q-model fully subsumes the Fama-French 6-factor model in head-to-head spanning tests. In the 1967-2018 monthly sample, the investment and Roe factors in the q-factor model earn on average 0.38% and 0.55% per month (t-value = 4.59 and 5.44), respectively. Their alphas in the Fama-French 6-factor model are 0.1% and 0.27% (t-value = 2.82 and 4.32), respectively. The Gibbons, Ross, and Shanken (GRS, 1989) test strongly rejects the null hypothesis that the 6-factor model can jointly subsume the investment and Roe factors (p-value = 0.00). Conversely, HML, CMA (the investment factor), RMW (the profitability factor), and UMD in the Fama-French 6-factor model earn on average 0.32%, 0.3%, 0.28%, and 0.64% per month (t-value = 2.42, 3.29, 2.76, and 3.73), respectively. More important, their alphas in the q-factor regressions are economically small (tiny in many cases) and statistically insignificant: 0.05%, 0.00%, 0.03%, and 0.14% (t-value = 0.49, 0.08, 0.32, and 0.61), respectively. The GRS test cannot reject the null hypothesis that the q-factor model can jointly subsume the HML, CMA, RMW, and UMD factors (p-value = 0.79). In all, despite having two fewer factors, the q-factor model fully subsumes the Fama-French 6-factor model, including UMD. Stambaugh and Yuan (2017) group 11 anomalies into two clusters based on pairwise cross-sectional correlations. The first cluster, denoted MGMT, contains net stock issues, composite issues, accruals, net operating assets, investment-to-assets, and the change in gross property, plant, and equipment plus the change in inventories scaled by lagged book assets. The second cluster, denoted PERF, includes failure probability, O-score, momentum, gross profitability, and return on assets. The composite scores, MGMT and PERF, are defined as a stock’s equal-weighted rankings across all the variables (realigned to yield positive low-minus-high returns) within a given cluster. Stambaugh and Yuan form their factors from monthly independent 2 by 3 sorts from interacting size with each of the composite scores. However, Stambaugh and Yuan (2017) deviate from the standard factor construction per Fama and French (1993) in two important ways. First, the NYSE-Amex-NASDAQ breakpoints of 20th and 80th percentiles are used, as opposed to the NYSE breakpoints of 30th and 70th, when sorting on the composite scores. Second, the size factor contains stocks only in the middle portfolios of the composite score sorts, as opposed to stocks from all portfolios. The Stambaugh-Yuan factors are sensitive to their factor construction, and their nonstandard construction exaggerates their factors’ explanatory power. Most important, once replicated via the standard procedure, the MGMT and PERF factors are close to the investment and Roe factors in the q-factor model, with correlations of 0.8 and 0.84, respectively (Hou, Mo, Xue, and Zhang, 2019a). Hou, Mo, Xue, and Zhang (2019b) perform cross-sectional forecasting regressions of future investment-to-assets changes on the log of Tobin’s q, operating cash flows, and the change in Roe. Independent 2 by 3 sorts on size and expected 1-year-ahead investment-to-assets changes yield an expected growth factor, with an average premium of 0.84% per month (t-value = 10.27) and a q-factor alpha of 0.67% (t-value = 9.75). Hou et al. augment the q-factor model with the expected growth factor to yield the model. Using a large set of 150 anomalies that are significant with NYSE breakpoints and value-weighted returns compiled in Hou, Xue, and Zhang (2019), Hou et al. conduct a large-scale horse race of latest factor models. The model is the best performing model that substantially outperforms the Fama-French (2018) 6-factor model. In fact, the q-factor model already compares well with the 6-factor model. However, unlike investment and profitability, expected growth is unobservable. The performance of the model depends on its expected growth specification, and crucially, on operating cash flows as a key predictor of future growth. As such, although its underlying intuition is clear, the model should be interpreted primarily as a tool for dimension reduction. Structural Estimation Factor models only explore directional predictions of the investment CAPM. In structural estimation, one takes the model’s key equation directly to the data for econometric estimation and evaluation. Hansen and Singleton (1982) conduct the first such test for the consumption CAPM. Liu, Whited, and Zhang (2009) perform the first structural estimation for the investment CAPM. Although by no means perfect, Liu et al.’s first stab yields much more encouraging results than Hansen and Singleton’s at the consumption CAPM. The baseline investment CAPM with only physical capital manages to explain value and post-earnings-announcement drift separately, albeit not jointly. Liu and Zhang (2014) show that the baseline model can explain Jegadeesh and Titman’s (1993) momentum separately, but not simultaneously with value. The joint estimation difficulty has been largely resolved by Goncalves, Xue, and Zhang (2019), who introduce working capital into the investment CAPM. With plausible parameter estimates, the two-capital investment CAPM manages to explain the value, momentum, investment, and Roe premiums jointly. Aggregation also plays an important role. Liu, Whited, and Zhang (2009) and Liu and Zhang (2014) construct portfolio-level predicted returns from portfolio-level accounting variables to match with portfolio-level stock returns. In contrast, Goncalves et al. use firm-level accounting variables to construct firm-level predicted returns, which are then aggregated to the portfolio level to match with portfolio-level stock returns. A surprising insight from Goncalves, Xue, and Zhang (2019) is that value and momentum (as well as investment and Roe) are driven by related, if not identical, mechanisms. Intuitively, current investment and expected investment are locked in a “tug of war” in the investment CAPM equation. When current investment overpowers expected investment, the model predicts the value and investment premiums. When expected investment overpowers current investment, the model predicts the momentum and Roe premiums. The predicted value and investment premiums are long-lived, persisting over 3-5 years after portfolio formation. The predicted momentum and Roe premiums are short-lived, vanishing within 1 year after portfolio formation. The model dynamics are intriguingly consistent with the dynamics in the data. Quantitative Theories Zhang (2005) constructs the first neoclassical, dynamic investment model for the cross section of returns in the spirit of real business cycles (Kydland and Prescott, 1982; Long and Plosser, 1983). Instead of estimating the first-order conditions formally in structural estimation, quantitative theory studies specify a dynamic model fully, calibrate and simulate it, and compare its implied moments with observed moments in the data. Zhang highlights the role of costly reversibility in explaining the value premium. Intuitively, value firms are burdened with more unproductive capital in bad times, finding it more difficult to downsize so as to yield more cyclical and riskier cash flows and earn higher expected returns than growth firms. In contemporaneous and independent work, Cooper (2006) shows closely related mechanisms at work in a real options model. Also in a related real options model, Carlson, Fisher, and Giammarino (2014) emphasize the role of operating leverage in driving the value premium. The Zhang model, recently labelled by Clementi and Palazzo (2019) as “the standard investment model,” has served as a launching pad for a large subsequent, theoretical literature on the cross section of returns. A full review of this literature is far beyond this analytical essay. A long-standing controversy in this theoretical literature is that the CAPM alpha of the value premium in Zhang’s (2005) model is economically small, although the average value premium itself matches that observed in the data. Subsequent studies have attempted to explain the failure of the CAPM in explaining the value premium in the post-Compustat sample by breaking the tight link between the stochastic discount factor (SDF) and the market factor with multiple aggregate shocks. Prominent examples include short- and long-run shocks (Ai and Kiku, 2013), investment-specific technological shocks (Kogan and Papanikolaou, 2013), stochastic adjustment costs (Belo, Lin, and Bazdresch, 2014). However, these 2-shock models all fail to explain the long sample evidence from 1926 onward that the CAPM alpha of the value premium is economically small and statistically insignificant. Bai, Hou, Kung, Li, and Zhang (2019) embed disasters into a general equilibrium model with heterogeneous firms to induce strong nonlinearity in the SDF to explain the CAPM failure. Intuitively, when a disaster hits, value firms are burdened with more unproductive capital, finding it more difficult with costly reversibility to reduce capital than growth firms. As such, value firms are more exposed to the disaster risk than growth firms, giving rise to a high average value premium. However, in a finite sample, in which disasters are not realized, the estimated market beta fails to fully capture the disaster risk embedded in the value premium. Consequently, the CAPM fails to explain the value premium in a finite sample without disasters. In the general equilibrium model of Bai, Hou, Kung, Li, and Zhang (2019), a nonlinear consumption CAPM holds by construction, yet the standard consumption CAPM fails badly in simulated data from the model. Intuitively, the aggregate consumption growth is a poor proxy for the SDF based on recursive utility. Their correlation in simulated data is close to zero. Surprisingly, the onset of disasters is not associated with particularly low contemporaneous consumption growth, and the onset of recoveries not with particularly high consumption growth. Intuitively, when a disaster hits, the SDF spikes up immediately because investors anticipate multiple years of high marginal utility (bad times). However, consumption smoothing immediately kicks in, with forward-looking real investment falling drastically to smooth consumption. Consequently, consumption only falls cumulatively over multiple years, making the contemporaneous consumption growth a bad proxy for the SDF. Relatedly, consumption smoothing also explains why the classic CAPM performs better than the standard consumption CAPM. Because stock prices are forward-looking, the market factor is much more correlated with the SDF than the contemporaneous consumption growth. A more recent controversy concerns the quantitative performance of the standard investment model (Zhang, 2005). Clementi and Palazzo (2019) argue that upon hit by adverse shocks, U.S. public firms have “ample latitude” to divest their unproductive assets. In particular, “each quarter on average 18.2% of firms record negative gross investment (p. 282),” suggesting that “plenty of firms downsize, at all times (p. 287),” and that there exists “no sign of irreversibility (p. 289).” Quantitatively, Clementi and Palazzo argue that for the standard investment model to explain the average value premium, its implied investment rates must be counterfactual, with a tiny fraction of negative rates and a cross-sectional volatility that is an order of magnitude smaller than that in the data. Bai, Li, Xue, and Zhang (2019) reexamine the evidence of costly reversibility in U.S. public firms. Bai et al. document that the firm-level investment rate distribution is highly skewed to the right, with a small fraction of negative investments, 5.79%, a tiny fraction of inactive investments, 1.46%, and a large fraction of positive investments, 92.75%. The firm-level evidence is even stronger than the prior plant-level evidence in Cooper and Haltiwanger (2006). Sample criteria likely play an important role. While Cooper and Haltiwanger include only relatively large manufacturing plants in continuous operations throughout their 1972-1988 sample, Bai et al. include virtually all Compustat firms in different industries (not just manufacturing), with no restrictions on size or age. With a careful replication effort, Bai, Li, Xue, and Zhang (2019) trace the differences between their evidence and Clementi and Palazzo’s (2019) to 3 sources. First, both studies measure gross investment rates as net investment rates plus depreciation rates. Both measure net investment rates as the net growth rates of net property, plant, and equipment (PPE) in Compustat. Bai et al. measure depreciation rates as Compustat’s depreciation over net PPE, depreciation rates that are embedded in net PPE. In contrast, Clementi and Palazzo use industry-level geometric depreciation rates estimated by Bureau of Economic Analysis, depreciation rates that are internally incompatible with net PPE in Compustat. Second, Clementi and Palazzo impose sample criteria that are nonstandard in empirical finance, such as removing firm-years with mergers and acquisitions, in which the target’s assets are more than 5% (a low cutoff) of the acquirer’s. Finally, Clementi and Palazzo also engage in a highly questionable research practice by cutting off the right tail of the quarterly investment rate distribution at 0.2. While Clementi and Palazzo’s (2019) evidence is flawed, their point of matching investment and returns moments jointly in quantitative studies is well taken. Using Simulated Method of Moments (SMM), Bai, Li, Xue, and Zhang (2019) estimate four parameters (the upward and downward adjustment cost parameters, the fixed cost of production, and the conditional volatility of firm-specific productivity) to target seven data moments (the average value premium, the cross-sectional volatility and skewness of individual stock excess returns, the cross-sectional volatility, skewness, and persistence of investment rates, as well as the fraction of negative investment rates). The SMM estimation strongly indicates costly reversibility and operating leverage in U.S. public firms. The downward adjustment cost parameter is estimated to be 508.2 (t-value = 13.39), which is substantially higher than the upward parameter, 0.63 (t-value = 4.6). The fixed cost of production is estimated to be 0.0637 (t-value = 4.24). The model matches the average value premium of 0.43% per month (t-value = 1.97) in the 1962–2018 sample. For investment rates, the cross-sectional volatility is 62% per annum (58.5% in the data) and the fraction of negative investments 5.78% in the model (5.79% in the data). The overidentification test fails to reject the model with the seven moments (p-value = 0.59). (This blog post is the first of a 4-part sequence based on my working paper fresh from the oven: "q-factors and investment CAPM, which is a solicited, analytical essay on the big-picture of the investment CAPM. Due to its length, I am splitting it into 4 parts on my blog. The link above gives the complete pdf, which also provides detailed references.)
Questions A voluminous literature in empirical asset pricing and capital markets research in accounting documents a wide range of relations between firm characteristics and average stock returns. These relations are often called “anomalies” because they cannot be explained by the standard consumption-based Capital Asset Pricing Model (the consumption CAPM), in which the classic Sharpe-Lintner CAPM (Sharpe, 1964; Lintner, 1965) is a special case. Prominent anomalies include post-earnings-announcement drift (Ball and Brown 1968; Bernard and Thomas 1989, 1990), long-term reversal (De Bondt and Thaler 1985), momentum (Jegadeesh and Titman 1993), long-term underperformance following initial and seasoned equity offerings (Ritter 1991; Loughran and Ritter 1995), the value anomaly (Lakonishok, Shleifer, and Vishny 1994), and the accrual anomaly (Sloan 1996). Behavioral economists interpret these anomalies as predictable pricing errors, which reject Fama’s (1970) efficient markets hypothesis (EMH) as well as Muth’s (1961) and Lucas’s (1972) rational expectations hypothesis. However, as emphasized by Fama (1991), anomalies do not necessarily reject EMH because the expected-return models used to isolate “pricing errors” in empirical tests can be incomplete (the joint-hypothesis problem). In particular, a coherent theory of inefficient markets with predictable pricing errors has yet to appear (Fama, 1998). Fama and French (1993, 1996) defend EMH by adding a size factor, SMB, and a value factor, HML, into the CAPM to form their 3-factor model. They interpret SMB and HML as sources of risk in the intertemporal CAPM (Merton, 1973) or Arbitrage Pricing Theory (APT) (Ross, 1976). However, this interpretation has not been persuasive. Both the intertemporal CAPM and APT are silent about the identities of state variables. As a result, SMB and HML are motivated from their empirical performance, rather than a priori theoretical arguments. Within this historical context, many fundamental questions arise. What explains all the CAPM anomalies? Why does the consumption CAPM fail so badly in explaining these anomalies? Given its abysmal performance, what confidence should one put in equilibrium theories that embed the consumption CAPM and permeate virtually all Ph.D. level textbooks in finance and economics? A prominent example is New Keynesian DSGE models. Graham and Dodd’s (1934) Security Analysis has worked for 85 years in practice. Why has it so far not found a rightful place in finance theory? Given that firm characteristics are so important in describing returns empirically, why do characteristics barely show up in finance theory? How should we interpret characteristics-based factors exactly? If anomalies are driven by expectation errors, what exactly are the psychological biases at play? Why do these systematic mistakes persist for so long, in some cases, such as post-earnings-announcement drift, for 50 years since Ball and Brown (1968)? Why has there not been a coherent theory of behavioral finance for almost 35 years since De Bondt and Thaler (1985)? An old science joke says: “Theory is when you know everything but nothing works. Practice is when everything works but no one knows why. In our lab, theory and practice are combined: Nothing works and no one knows why.” Finance is better. The consumption CAPM theory is well developed, but it doesn’t work. Anomaly strategies work, but no one knows why. In the investment CAPM, theory and practice are combined: Everything works and I know why. Mechanisms The basic philosophy of the investment CAPM is to price risky assets from the perspective of their suppliers (firms), as opposed to their buyers (investors) (Zhang, 2017), building on an early precursor of Cochrane (1991). Mathematically, the investment CAPM is a restatement of the Net Present Value (NPV) rule in Corporate Finance. The NPV of a project is its present value (discounted value of its future cash flows) minus its investment costs today. The NPV rule says that a manager should invest in a given project if and only if its NPV is greater than or equal to zero. When initially facing many projects with NPV ≥ 0, the manager will start with the project with the highest NPV and work her way down the supply curve of projects. For the last project that the manager takes, its NPV should equal zero. To keep things simple, consider first one-period projects. The last project with NPV = 0 means that its investment costs = profitability / discount rate. The investment CAPM turns the NPV rule, which is a fundamental principle in Corporate Finance, on its head and transforms it into an Asset Pricing theory. Rewriting the NPV rule yields: Discount rate = profitability / investment costs. Intuitively, given profitability, high costs of capital (discount rates) imply low NPVs of new projects and low investments, and low costs of capital imply high NPVs of new projects and high investments. In addition, given investments, high profitability must imply high discount rates to give rise to low NPVs of new projects to keep investments constant. Low profitability relative to investments must imply low discount rates to offset low profitability to keep the NPVs of new projects and investments constant. In all, investment and profitability are two key drivers in cross section of expected returns. If projects last more than one period as in a multiperiod model, the NPV rule becomes: Investment costs = (profitability + present value of cash flows from next period onward) / discount rate. With optimal investment, the present value of cash flows from next period onward equals expected investment costs next period (marginal q equals marginal costs of investment). As such, the investment CAPM says: Discount rate = (profitability + expected investment costs) / investment costs. Intuitively, if investment and expected investment costs are high next period, the present value of cash flows from next period onward must be high. Consisting primarily of this next period present value, the benefits to investment this period must also be high. As such, if investment is high next period relative to current investment (expected investment growth is high), the discount rate must be high. The discount rate must be high to offset the high benefits of investment this period to keep current investment low. As such, expected growth is another key driver in the cross section of expected stock returns. Kewei, Chen, and I have finally launched our q-factors data library at:
global-q.org The old google site at "https://sites.google.com/site/theqfactormodel/" listed on the title page of Hou, Xue, and Zhang (2015, Review of Financial Studies) has been deleted. As a first step, the new data library site contains our q-factors series as well as testing portfolios formed on 50 anomaly variables, a subset from Hou, Xue, and Zhang ("Replicating anomalies," forthcoming, Review of Financial Studies). We will post more data online as our empirical work progresses. Thank you for your patience! Please feel free to drop us an email if you have comments on the data library and/or our work. A cool friend of mine on Twitter, Drew Dickson at Albert Bridge Capital, joined in the latest exchange between behavioral finance and EMH with a nice post titled “Behavioral Finance Is Finance.” Drew is kind enough to cite my first blog post titled “Fama Is Right” in his article. Thank you Drew. I very much appreciate your kindness, seriousness, and thoughtfulness that permeate your writing. I find many of your points to be quite reasonable. And I take them very seriously. In this blog I argue that the newly developed investment literature has provided (or at least started to provide) answers to many of the important questions that Drew has raised. In no way I think my answers are complete or perfect. I am keenly aware of several remaining issues and I am actively working to resolve them. Most important, I value the opportunities to learn about others’ perspectives, especially those from asset managers with whom I don’t interact daily. I am fully capable of admitting mistakes when proven wrong. I am not very good at listening but I am trying. In what follows, I first quote directly from Drew's article and then provide point-by-point responses. “Does behavioral finance need to figure out a model of market equilibrium that makes markets efficient? Isn’t that a bit of a diversion? Hasn’t behavioral finance actually provided a theoretical underpinning for many of the most successful ‘factors’? Hasn’t behavioral finance made relevant these theory-less multi-factor models of market equilibrium?” Please let me clarify my perspective. Start with the accounting identity: Realized returns = expected returns + abnormal returns. When an anomaly variable forecasts realized returns, there are automatically two parallel interpretations. One, which is the behavioral view, says that the variable is forecasting abnormal returns. As such, pricing errors are forecastable, yielding a violation of EMH. The other, which is the EMH view, says that the anomaly variable is related to expected returns but the errors are unpredictable. The consumption CAPM and the investment CAPM are both about expected returns. Both are consistent with EMH. When I say no behavioral theory since 1985, I meant no theory of “abnormal returns.” If behavioral finance is to become a competing paradigm with EMH, the burden seems to be on its proponents to develop a theory of abnormal returns. Such a model doesn’t make markets efficient. It would be a theory of inefficient markets, a theory of pricing errors. And it’s not a diversion. It's the essence of behavioral finance. Why do investors make the same mistakes repeatedly year after year? When I say “equilibrium,” I don’t mean fancy math. I just meant prices being jointly determined by supply and demand. Like gravity, there is no escape from this law. How much you pay for your new house depends on whether the seller has a competing offer and whether you have in mind a backup house that you and your family like. There are indeed behavioral theories that link value and momentum to different psychological biases. However, these models all assume a constant discount rate (expected return). While a useful first stab, these models basically assume that all the return predictability in the data arises from predictable pricing errors. This is why many economists feel that the existing behavioral models just relabel things. More on this point later. “And it’s provided plenty of evidence that markets don’t always get things right. And frankly, there is very little supporting evidence of the risk story behind many of Fama and French’s proposed factors. Size? Maybe (big maybe). But why is value riskier than growth? Why are firms with better gross profitability riskier than those that are less profitable? Why are firms that efficiently invest capex more risky?” “And perhaps a more important, and bigger, question: why didn’t Fama and French include momentum in either their three or five factor models? They know it’s there. They know it’s a thing.” “The answer, because there is almost no possible risk explanation for momentum. The behavioral guys have plenty of reasons. They have common sense, intuitive reasons; motives like loss aversion, confirmation bias, anchoring and herding. Even Fama himself has admitted that momentum ‘is an embarrassment to the theory.’ Momentum isn’t embarrassing for Narasimhan Jegadeesh, Sheridan Titman, Cliff Asness, or Mark Carhart. Momentum isn’t embarrassing for those who know that behavioral finance hasn’t been a failure. For those guys, momentum is beautiful.” Very cool questions. Thank you. I respect and appreciate your frank communication. It is only through frank communication will I learn where my arguments fall short. I’ve been thinking about the same questions for 20 years ever since I started to do research in 1999 as a second-year Ph.D. student at Wharton. In what follows, I summarize my current, still evolving thoughts. I think I have reasonable answers. Again, in no way I think my answers are perfect. Please feel free to let me know where I screw up. So I can try to improve going forward. Momentum is a success story for the investment CAPM. As shown in the table below, UMD can be explained by the q-factor model in Hou, Xue, and Zhang (2015). The average return of UMD is 0.64% per month in the 1967-2018 sample, but its q-factor alpha is only 0.14%, with an insignificant t-value of 0.61. The return on equity (Roe) factor plays a major role in explaining UMD. The evidence shows that momentum is a noisy version of our Roe factor. Intuitively, the Net Present Value rule in capital budgeting says that high expected Roe relative to low current investment should imply high costs of capital (expected returns). And current Roe is a proxy for the expected Roe. That’s it.
The difficulty arises as for what risks lurk behind momentum. I could follow Fama and French (1993) and call the q-factor loadings risk measures. And it will be correct from a statistical standpoint such as APT. But from an economic standpoint, I feel that a more precise interpretation of the q-factor model should be a linear factor approximation of the nonlinear characteristic model of the investment CAPM (Lin and Zhang 2013; Zhang 2017). However, I acknowledge that the investor-side CAPM and the supplier-side CAPM should be internally consistent. While the supplier-side CAPM is worked out in theory and in the data, it would be better if it can be demonstrated what exactly the risks are lurking behind the investor-side CAPM, at least conceptually. There are a few rational models floating around at this point, such as Johnson’s (2002) expected growth and Sagi and Seasholes’s (2004) growth options. And I have done a few econometric studies that link momentum to expected investment growth (Liu and Zhang 2014; Goncalves, Xue, and Zhang 2019). Intuitively, momentum winners have higher expected growth than momentum losers. And the expected growth is risky (to the extent that it might not be materialized). However, an important weakness of the current theoretical literature is that it lacks a unified equilibrium theory of value and momentum together. Li (2018) is the only example I can think of. We should work more to figure out the exact sources of risks behind expected growth (and momentum and Roe factors). In short, momentum is not a problem per se from the supply-side investment CAPM. Alas, a significant gap in our knowledge exists in terms of exactly how momentum can be consistent with the consumption CAPM in a fully specified model. As challenging as it is, I don't view it as insurmountable, however. Finally, as an economist, I have some preferences over an optimization-based model. Gene said in his latest interview that behavioral economists reply on investors being “stupid, repeatedly stupid.” Gene is right, in my view. Regardless of how sensible, intuitive the underreaction explanation might appear at a first glance, it’s hard to believe, for me at least, that investors would be confused for more than 50 years about post-earnings-announcement drift since Ball and Brown (1968). Once the horizon is that long, the biases explanation no longer feels sensible or intuitive. The fact that the drift persists for so long indicates to me that it is in fact part of the expected returns. “Behavioral economics is no longer the domain of rogue traitors attacking efficient market theory. Behavioral economists are the patriots of finance.” Bravo. I totally agree. I feel sorry that you even felt the need to make this statement. There is no question whatsoever in my mind that behavioral economists are patriots of finance. Thaler, Bernard, Thomas, Jegadeesh, Titman, Lakonishok, Sloan, and Ritter are heroes in my book. Reconciling their enormous contributions with what I learned in school has been my life’s endeavor. I’m very much indebted to them. I am very familiar with the role of a “traitor.” I am just doing my “betraying” in a different way. Alas, challenging the status quo is the essence of research. I feel that I have something new and important to say. And that’s the source of all my “treachery.” Behavioral finance is no longer a fringe field. It’s mainstream. Just like EMH before the rise of behavioral finance, a mainstream school of thoughts provides a ready target for the next generation of “traitors.” So get ready for more. I agree with behavioral finance on the facts (barring Hou, Xue, and Zhang 2019, "Replicating anomalies") but disagree on their interpretation. I know this is exactly what Gene said. But unlike Gene, I have theory, in addition to evidence, to back me up. I challenge my professional colleagues to prove me wrong, scientifically. References Ball, Ray, and Philip Brown, 1968, An empirical evaluation of accounting income numbers, Journal of Accounting Research 6, 159-178. Fama, Eugene F., and Kenneth R. French, 1993, Common risk factors in the returns on stocks and bonds, Journal of Financial Economics 33, 3–56. Goncalves, Andrei S., Chen Xue, and Lu Zhang, 2019, Aggregation, capital heterogeneity, and the investment CAPM, forthcoming, Review of Financial Studies. Hou, Kewei, Chen Xue, and Lu Zhang, 2015, Digesting anomalies: An investment approach, Review of Financial Studies 28, 650-705. Hou, Kewei, Chen Xue, and Lu Zhang, 2019, Replicating anomalies, forthcoming, Review of Financial Studies. Johnson, Timothy C., 2002, Rational momentum effects, Journal of Finance 57, 585-608. Li, Jun, 2018, Explaining momentum and value simultaneously, Management Science 64, 4239-4260. Lin, Xiaoji, and Lu Zhang, 2013, The investment manifesto, Journal of Monetary Economics 60, 351-366. Liu, Laura X. L., and Lu Zhang, 2014, A neoclassical interpretation of momentum, Journal of Monetary Economics 67, 109-128. Sagi, Jacob S., and Mark S. Seasholes, 2007, Firm-specific attributes and the cross-section of momentum, Journal of Financial Economics 84, 389-434. Zhang, Lu, 2017, The investment CAPM, European Financial Management 23, 545-603. (An earlier, shorter version of this article appeared earlier today on alphaarchitect.com under the title “Investment, Expected Investment, and Expected Stock Returns”. I thank Wes Gray for soliciting the article.) A new DFA article by Rizova and Saito (2019) titled “Investment and Expected Stock Returns” rehashes old (in my view, largely discredited) arguments by Fama and French (2006, 2015) on the investment factor: i) Valuation theory predicts that expected investment is negatively correlated with expected return, all else equal; and ii) Current asset growth is a good proxy for expected investment. According to Fama and French, the negative relation between expected investment and expected return then gives rise to the investment factor, which captures the negative relation between current investment and expected return in the data. Based on Hou et al. (2019a), this blog shows that Fama and French’s arguments are fundamentally flawed. I also summarize the conceptual foundation of Hou, Xue, and Zhang's (2015) investment factor, a foundation which in my view better captures the underlying economics of the investment factor. A Positive Relation between Expected Investment and Expected Return in Valuation Theory In Fama and French’s formulation of valuation theory, the discount rate is the internal rate of return, which is constant over time. While a useful concept, the constant discount rate return clearly contradicts the well accepted notion of time-varying expected returns. For instance, it is nowadays well accepted that expected returns are most likely higher in recessions than in booms. Expected momentum profits are reliably positive but only within one year post-formation and are negative afterward. Hou et al. (2019a) reformulate valuation theory with one-period-ahead expected return. They show that the relation between expected investment and the one-period-ahead expected return is more likely to be positive in the reformulated valuation theory. See their paper for the detailed derivations. Empirically, Fama and French (2006) in fact report a positive, albeit weak, relation between expected investment and expected return. They write: “Contrary to the predictions of the valuation equation (3), however, the return regressions of Table 3 produce positive average slopes on the Table 2 regression proxies for expected asset growth, but they are not reliably different from zero (p. 507).” Specifically, in their Table 3, which is reproduced below, the highlighted column below is the slopes on expected investment in monthly cross-sectional return regressions. The slopes are mostly positive, albeit insignificant. The evidence says that expected investment estimated via their specifications is positively related to the expected return, although the relation is weak. Table 3 in Fama and French (2006): Monthly cross-sectional return regressions Current Asset Growth Is a Poor Proxy for Expected Investment Continuing on the (in my view, wrong) path of a negative relation between expected investment and expected return, Fama and French (2015) ditch the two specifications of expected investment in Table 2 of their 2006 article and switch to current asset growth as the proxy for expected investment. Doing so yields a desired negative relation between expected investment and expected return. However, current asset growth is all but a poor proxy for expected investment. The evidence is borne out in Table 2 in Fama and French (2006) reproduced below. The table shows annual cross-sectional regressions of future asset growth on lagged firm variables, one of which is current asset growth. If asset growth is a perfect proxy for expected asset growth, the slopes on current asset growth should be close to one and drive out all other variables. However, the first highlighted column below does not support this view. In the shorter specification, the slopes on asset growth are economically small, albeit significant, indicating only weakly positive autocorrelations of asset growth. In the longer specification, the slopes on asset growth are all virtually zero and insignificant. Table 2 in Fama and French (2006): Multiple regressions to predict asset growth Further evidence is provided in Table VII in Hou et al. (2019a) reproduced below. The table shows annual cross-sectional regressions of book equity growth on current asset growth and, separately, on current book equity growth. The first highlighted column shows that the slopes on current investment when predicting future investment are far from one, 0.2 in the first year, and quickly falls toward zero afterward. The R-square starts at 6% in year one and falls largely to zero afterward. Table VII in Hou et al. (2019a): Annual cross-sectional regressions of future book equity growth and future operating profitability The last five columns in the table above show the cross-sectional regressions of operating profitability on current operating profitability. Operating profitability is substantially more persistent than investment, the slope in the first year is 0.8, and the R-square 0.54. This evidence supports Fama and French’s (2015) use of operating profitability as expected operating profitability in their 5- and 6-factor models as well as Hou, Xue, and Zhang’s (2015) use of current return on equity (Roe) as expected Roe in the q-factor model. In particular, earnings are often characterized as a random walk in the accounting literature. In sum, the evidence is clear that current asset growth is a poor proxy for expected asset growth, but current operating profitability is a good proxy for expected operating profitability. The evidence refutes Fama and French’s (2015) arguments of the investment factor via the expected investment channel. Investment, Expected Investment, and Expected Stock Returns: The Investment CAPM Perspective In the investment CAPM (Zhang 2017), investment and expected investment are related to expected return in two opposite ways. Hou, Xue, and Zhang (2015) propose the investment factor as a key driving force of expected stock returns. In Corporate Finance, the net present value (NPV) of a project is its present value (discounted value of the project’s future cash flows) minus its investment costs today. The NPV rule says that a manager should invest in a given project, if and only if the present value of the project is greater than or equal to its investment costs. When initially facing many projects with nonnegative NPVs, the manager should start with the project with the highest NPV and work her way down the supply curve of projects. A good project has a low discount rate, high profitability, and low investment costs. As the manager takes more and more projects, their investment costs become higher and higher, and their profitability lower and lower. For the last project that the manager takes, its NPV should equal zero: (A) Investment costs = Present value = Profitability/Discount rate. The investment CAPM turns the NPV rule, which is a fundamental principle in Corporate Finance, on its head and transforms it into an Asset Pricing theory. Rewriting the NPV rule yields: (B) Discount rate = Profitability/Investment costs. Relative to profitability, high investment firms incur higher investment costs, meaning that their discount rates and expected returns must be low. Relative to investment, high profitability firms must have high discount rates and high expected returns. In all, investment and profitability are two key driving forces of expected stock returns. The investment factor arises naturally from equation (B). Intuitively, given profitability, high costs of capital (discount rates) imply low NPVs of new projects and low investments, and low costs of capital imply high NPVs of new projects and high investments. Equations (A) and (B) apply to a static model with only one period. In a multiperiod, dynamic model, equation (A) becomes: (A’) Investment costs = Present value = (Profitability + Present value of cash flows from next period onward)/Discount rate. However, with optimal investment, the present value of cash flows from next period onward equals expected investment costs next period (marginal q equals marginal costs of investment). Accordingly, equation (B) becomes: (B’) Discount rate = (Profitability + Expected investment costs)/Investment costs. Intuitively, if investment and expected investment costs are high next period, the present value of cash flows from next period onward must be high. Because the benefits to investment this period are primarily the present value from next period onward, the benefits to investment this period must also be high. As such, if expected investment costs are high next period relative to investment costs this period, or equivalently, if expected investment is high next period relative to current investment, the discount rate must be high. The discount rate must be high to offset the high benefits of investment this period to keep current investment low. This intuition behind the positive relation between expected investment (growth) and expected return is analogous to the intuition behind the positive relation between profitability and expected return, i.e., the Roe factor in the q-factor model. And this is the core intuition underlying the expected investment growth factor in the q^5 model of Hou et al. (2019b). Factor Spanning Tests: The q-factor model versus the Fama-French (2018) 6-factor model The following table updates Hou et al.'s (2019a) factor spanning tests. The tests show that the q-factor model cleanly subsumes the Fama-French 6-factor model in head-to-head contests. Specifically, in the 1967-2018 monthly sample, the investment and return on equity (Roe) factors in the q-factor model earn on average 0.38% and 0.55% per month (t = 4.59 and 5.44), respectively. Their alphas in the Fama-French 6-factor regressions are 0.1% and 0.27%, both of which are significant (t = 2.82 and 4.32), respectively. The Gibbons, Ross, and Shanken (GRS, 1989) test strongly rejects the null hypothesis that the Fama-French 6-factor model can subsume the investment and Roe factors. In all, despite having two more factors, the Fama-French 6-factor model cannot subsume the q-factor model in the data.
Conversely, HML, CMA, RMW, and UMD in the Fama-French 6-factor model earn on average 0.32%, 0.3%, 0.28%, and 0.64% per month (t = 2.42, 3.29, 2.76, and 3.73), respectively. More important, their alphas in the q-factor regressions are economically small (tiny in many cases) and statistically insignificant: 0.05%, 0.00%, 0.03%, and 0.14% (t = 0.49, 0.08, 0.32, and 0.61), respectively. The GRS test cannot reject the null hypothesis that the q-factor model can subsume the HML, CMA, RMW, and UMD factors. In all, despite having two fewer factors, the q-factor model fully subsumes the Fama-French 6-factor model, including UMD. Summary Fama and French’s (2006, 2015) arguments for the investment factor are fundamentally flawed. Valuation theory, once reformulated in terms of the one-period-ahead expected return, implies a positive relation between expected investment and expected return, a prediction which Fama and French’s (2006) evidence also indicates. In addition, unlike profitability, firm-level asset growth is not (that) persistent, meaning that current asset growth is a poor proxy for expected investment. Most tellingly, Fama and French (2018) seem to have abandoned any theoretical discipline when adding the momentum factor, UMD, into their 6-factor specification: "We include momentum factors (somewhat reluctantly) now to satisfy insistent popular demand. We worry, however, that opening the game to factors that seem empirically robust but lack theoretical motivation has a destructive downside: the end of discipline that produces parsimonious models and the beginning of a dark age of data dredging that produces a long list of factors with little hope of sifting through them in a statistically reliable way (p. 237, my emphasis)." In contrast, the investment factor arises naturally from the investment CAPM, which in essence is a restatement of the Net Present Value rule in Corporate Finance. Intuitively, given profitability, high costs of capital (discount rates) imply low NPVs of new projects and low investments, and low costs of capital imply high NPVs of new projects and high investments. In all, it is perhaps time to embrace the supply approach to asset pricing to distill some theoretical discipline that the field of empirical asset pricing has been sorely lacking since, well, Fama and French (1993). After all, empirically, factor spanning tests show that the q-factor model fully subsumes the Fama-French 6-factor model in head-to-head contests. References Fama, Eugene F., and Kenneth R. French, 1993, Common risk factors in the returns on stocks and bonds, Journal of Financial Economics 33, 3–56. Fama, Eugene F., and Kenneth R. French, 2006, Profitability, investment and average returns, Journal of Financial Economics 82, 491-518. Fama, Eugene F., and Kenneth R. French, 2015, A five-factor asset pricing model, Journal of Financial Economics 116, 1-22. Fama, Eugene F., and Kenneth R. French, 2018, Choosing factors, Journal of Financial Economics 128, 234-252. Gibbons, Michael R., Stephen A. Ross, and Jay Shanken, 1989, A test of the efficiency of a given portfolio, Econometrica 57, 1121–1152. Hou, Kewei, Haitao Mo, Chen Xue, and Lu Zhang, 2019a, Which factors? Review of Finance 23, 1-35. Hou, Kewei, Haitao Mo, Chen Xue, and Lu Zhang, 2019b, q^5, working paper, The Ohio State University. Hou, Kewei, Chen Xue, and Lu Zhang, 2015, Digesting anomalies: An investment approach, Review of Financial Studies 28, 650-705. Rizova, Savina, and Namiko Saito, 2019, Investment and expected stock returns, Dimensional Fund Advisors. Zhang, Lu, 2017, The investment CAPM, European Financial Management 23, 545-603. A Facebook friend of mine forwarded me a video clip of Gene Fama’s latest interview on Bloomberg with Barry Ritholtz. I watched the full interview just now. And it occurs to me that I might have a few relevant things to say about the important issues discussed in the interview. The high point (or low point, depending on whom you ask) of the interview is when Gene says: “There is no behavioral finance. It’s all just a criticism of efficient markets, with no evidence.” Gene went on to clarify that 20 years ago, he challenged behavioral finance to come up with a theory that people can take to the data and test (Fama 1998). Fast forward to 20 years later, we are still waiting. Gene’s statement has caused an uproar on the internet. In particular, Dick Thaler responded with the following tweet: To no one’s surprise, I find myself mostly in agreement with Gene. I would drop the bit “with no evidence” but I find Gene’s statement to be accurate. The case for behavioral finance is extremely weak. On the theoretical side, it has been almost 35 years since De Bondt and Thaler (1985), yet there is still not a single coherent behavioral theoretical framework in sight, not to say its structural estimation that takes the theory to the data. Ideally, one would like to identify exactly what psychological biases are in play, the specific mechanisms via which the biases impact on equilibrium prices, and formal econometric estimation and tests to quantify the mechanisms in the data. Sure, there have been sporadic theoretical efforts, but the resulting models are typically so ad hoc (and so disconnected among themselves) that they have mostly been tested in an informal, reduced form way. On the empirical side, EMH says that pricing errors are not forecastable. I view EMH as equivalent to the Muth-Lucas rational expectations, which says that forecasting errors are not forecastable (a hat tip to my Wharton advisors' long-lasting influence on my work). Now, for the rubber to hit the road, one has to bundle EMH with an expected return model to isolate “pricing errors” or abnormal returns. The empirical literature has traditionally adopted the classic CAPM for this purpose and found its empirical performance to be lacking. The consumption CAPM performs even more poorly and remains mostly in theoretical papers on narrower topics. The Fama-French 3-factor model took over in 1993 as the workhorse empirical model, but the interpretation of SMB and HML is unclear. In all, the contribution of behavioral finance, which I acknowledge to be enormous, is to demonstrate the empirical failures of the (consumption) CAPM. However, the evidence does not reject EMH, at least not directly (the ubiquitous joint-hypothesis problem). During the past 20 years, instead of behavioral finance, it is investment-based asset pricing that has risen up to meet Fama’s (1998) challenge. And this newer literature has done so within the scope of EMH. The key insight of the investment literature is to price risky assets from the perspective of their suppliers (firms), as opposed to their buyers (investors) (Zhang 2017). Buyers are heterogeneous in preferences, beliefs, and information sets, all of which make the buy-side pricing exceedingly difficult. This statement just reflects the classic, largely intractable aggregation problem in equilibrium theory (the Sonnenschein-Mantel-Debrew theorem). Who’s the marginal investor of Apple Inc.? Your guess is as good as mine. On the supply side, who’s the marginal supplier of Apple Inc.? Well, easy, that’s Apple Inc. No aggregation difficulty even remotely in the same magnitude as that plaguing the (consumption) CAPM (or any other demand-based theories). As a new class of Capital Asset Pricing Models, the investment CAPM arises from the first principle of real investment for individual firms. Building on the first principle, the investment CAPM is every bit as rigorous as any economic theory that I am aware of, including, in particular, the consumption CAPM. The academic literature has been evaluating the empirical, explanatory power of the investment CAPM in the past decade. The evidence so far seems rather encouraging. Hou, Xue, and Zhang (2015) motivate the investment and return on equity factors in the q-factor model from the investment CAPM. Close cousins of the q-factor model have subsequently appeared in different disguises in the Fama-French (2015, 2018) 5- and 6-factor model, the Stambaugh-Yuan (2017) “mispricing” factor model, and the Daniel-Hirshleifer-Sun (2019) behavioral 3-factor model. See Hou et al. (2019a) for a detailed exposition. In particular, the following table shows that the 4-factor q-model fully subsumes the Fama-French 6-factor model in head-to-head factor spanning tests. In terms of structural estimation, Liu, Whited, and Zhang (2009) perform the first such estimation of the investment CAPM in a way that is analogous to what Hansen and Singleton (1982) did for the consumption CAPM. Although by no means perfect, Liu et al.’s first stab yields much more encouraging results than Hansen and Singleton’s at the consumption CAPM. The baseline investment model with only physical capital manages to explain value and momentum separately, albeit not jointly. The joint estimation difficulty has been largely resolved in Goncalves, Xue, and Zhang (2019), who introduce working capital into the investment framework. With plausible parameter estimates, the two-capital investment model manages to explain the value, momentum, investment, and return on equity premiums simultaneously. The next step is to investigate out-of-sample performance and to develop an ex-ante, expected return model that can compete with the implied costs of capital from the accounting literature.
I view the investment CAPM and the consumption CAPM as complementary in theory. Marshall (1890, Principles of Economics) writes: “We might as reasonably dispute whether it is the upper or under blade of a pair of scissors that cuts a piece of paper, as whether value is governed by utility or costs of production. It is true that when one blade is held still, and the cutting is affected by moving the other, we may say with careless brevity that the cutting is done by the second; but the statement is not strictly accurate, and is to be excused only so long as it claims to be merely a popular and not a strictly scientific account of what happens (Marshall, 1890 [1961, 9th edition, p. 348]).” Clearly, by only looking at demand, the consumption CAPM is incomplete even in theory. The investment CAPM is the missing “blade.” The covariance, SDF-centric view of the world only describes the optimal demand behavior. The supply side is all about characteristics. So much for the covariances versus characteristics debate. In my big-picture, there is no obvious place for behavioral finance. The field has gained its prominence by documenting non-zero means of the CAPM residuals and sticking labels such as under- and over-reaction to them. However, the evidence has been piling up that the investment CAPM alphas are not that big to begin with. I should acknowledge that the investment CAPM is silent about investor rationality. And that’s the whole point. Investor rationality and EMH are two different things. Remember EMH only says that pricing errors are not forecastable. The investment CAPM alphas are mostly not forecastable. And the expectations in the investment CAPM are entirely rational. Investors might be optimistic and attempt to bid up the equity prices too high. But with a manager’s cool head, the supply of risky shares goes up. In the special case of no adjustment costs, in particular, Tobin’s q will forever be one, regardless of how irrationally optimistic investors are. This equilibrating role of the supply side seems to be greatly underappreciated in the existing literature. We are blind to this parallel universe thanks to the consumption CAPM's single-minded, dogmatic focus on demand. I can empathize that after more than 50 years of the classic CAPM, it’s intellectually hard to divorce EMH from the (consumption) CAPM. But the (consumption) CAPM is just the blunt “blade” due to its inescapable, intractable problem of aggregation. After marrying EMH with the sharp “blade” of the investment CAPM, we see that capital markets simply obey standard economic principles. The world makes sense! Investor behavior is a separate, important field, but is partial equilibrium in nature. Without tackling aggregation, investor behavior has close to nothing to say about equilibrium pricing. Again, investor rationality and EMH are not the same thing. I certainly do not agree with everything that Gene said in the interview. Wall Street research is definitely not “business-related pornography.” Financial analysts are an important component of financial intermediary that facilitates the information flow and smooth functioning of our capital markets. Graham and Dodd’s (1934) Security Analysis works in the data, as shown by a mountain of evidence in the accounting literature. And it is perfectly consistent with the investment CAPM, which predicts cross-sectionally varying expected returns, depending on investment, profitability, and expected growth (Hou et al. 2019b). In Thaler’s tweet, he claims that Gene owes him everything. I think Dick got the chronology exactly backward. Gene founded modern finance with EMH, against which Dick has successfully built his entire career. If anything, Dick owes Gene everything. I, on the other hand, owe much of my career to behavioral finance, whose tremendously important empirical contributions, with little in the way of theory, have left a glaring gulf for a theory-minded economist to fill. References Daniel, Kent D., David Hirshleifer, and Lin Sun, 2019, Short- and long-horizon behavioral factors, forthcoming, Review of Financial Studies. De Bondt, Werner F. M., and Richard Thaler, 1985, Does the stock market overreact? Journal of Finance 40, 793-805. Fama, Eugene F., 1998, Market efficiency, long-term returns, and behavioral finance, Journal of Financial Economics 49, 283-306. Fama, Eugene F., and Kenneth R. French, 2015, A five-factor asset pricing model, Journal of Financial Economics 116, 1–22. Fama, Eugene F., and Kenneth R. French, 2018, Choosing factors, Journal of Financial Economics 128, 234–252. Goncalves, Andrei S., Chen Xue, and Lu Zhang, 2019, Aggregation, capital heterogeneity, and the investment CAPM, forthcoming, Review of Financial Studies. Graham, Benjamin, and David L. Dodd, 1934, Security Analysis, 1st ed., New York: Whittlesey House, McGraw-Hill Book Company. Hansen, Lars P., and Kenneth J. Singleton, 1982, Generalized instrumental variables estimation of nonlinear rational expectations models, Econometrica 50, 1269–1288. Hou, Kewei, Haitao Mo, Chen Xue, and Lu Zhang, 2019a, Which factors? Review of Finance 23, 1–35. Hou, Kewei, Haitao Mo, Chen Xue, and Lu Zhang, 2019b, Security analysis: An investment approach, working paper, The Ohio State University. Hou, Kewei, Chen Xue, and Lu Zhang, 2015, Digesting anomalies: An investment approach, Review of Financial Studies 28, 650-705. Liu, Laura X. L., Toni M. Whited, and Lu Zhang, 2009, Investment-based expected stock returns, Journal of Political Economy 117, 1105-1139. Marshall, Alfred, 1890, Principles of Economics (9th ed.) (London: Macmillan, first published in 1890, 1961). Stambaugh, Robert F., and Yu Yuan, 2017, Mispricing factors, Review of Financial Studies 30, 1270–1315. Zhang, Lu, 2017, The investment CAPM, European Financial Management 23, 545-603. |
Lu Zhang
An aspiring process metaphysician Archives
September 2025
Categories |


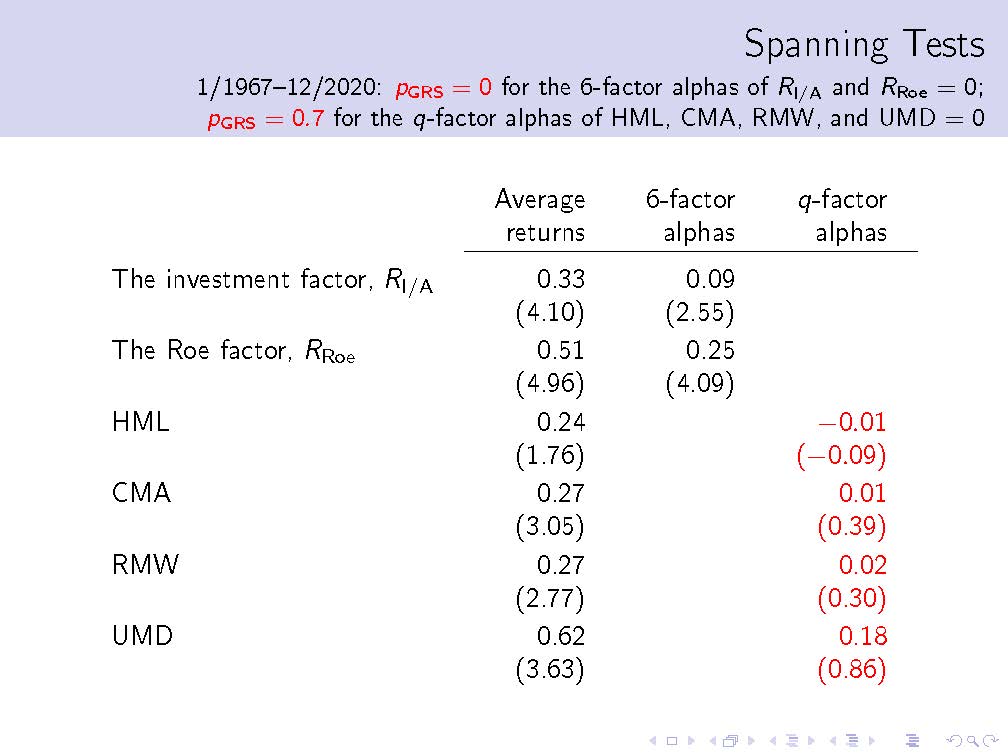
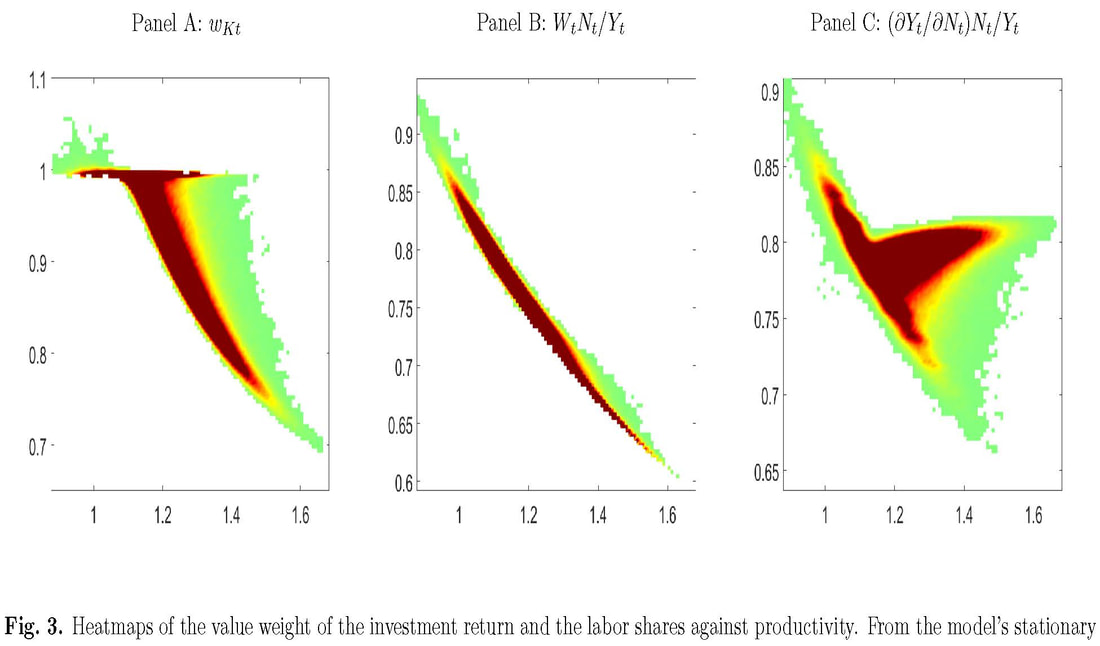
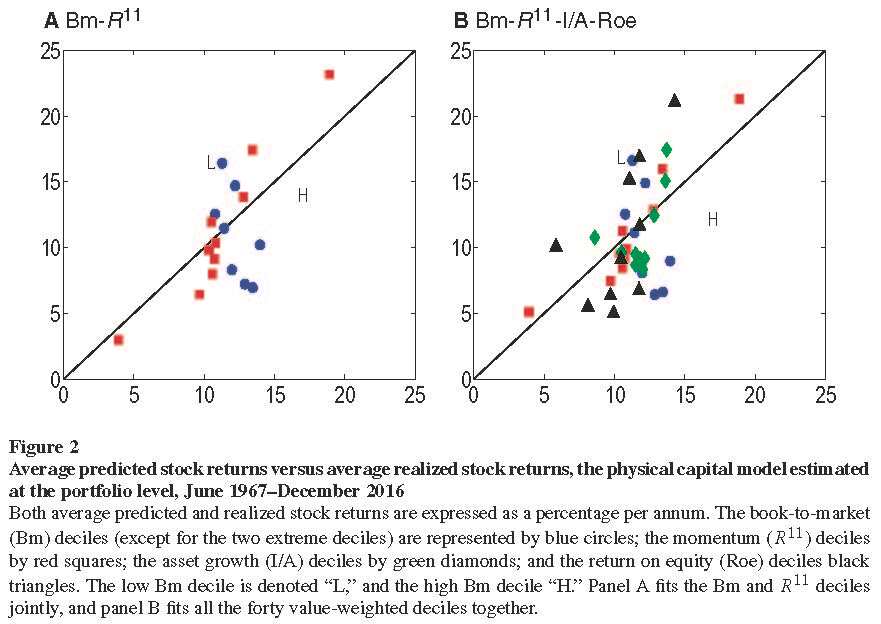



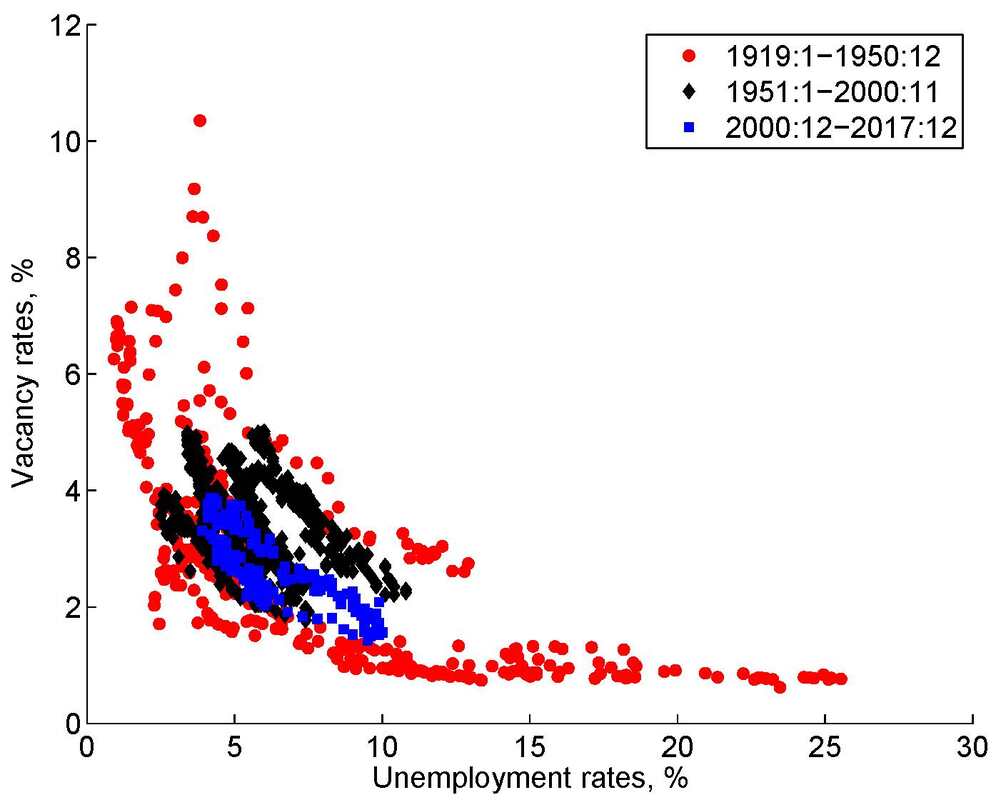


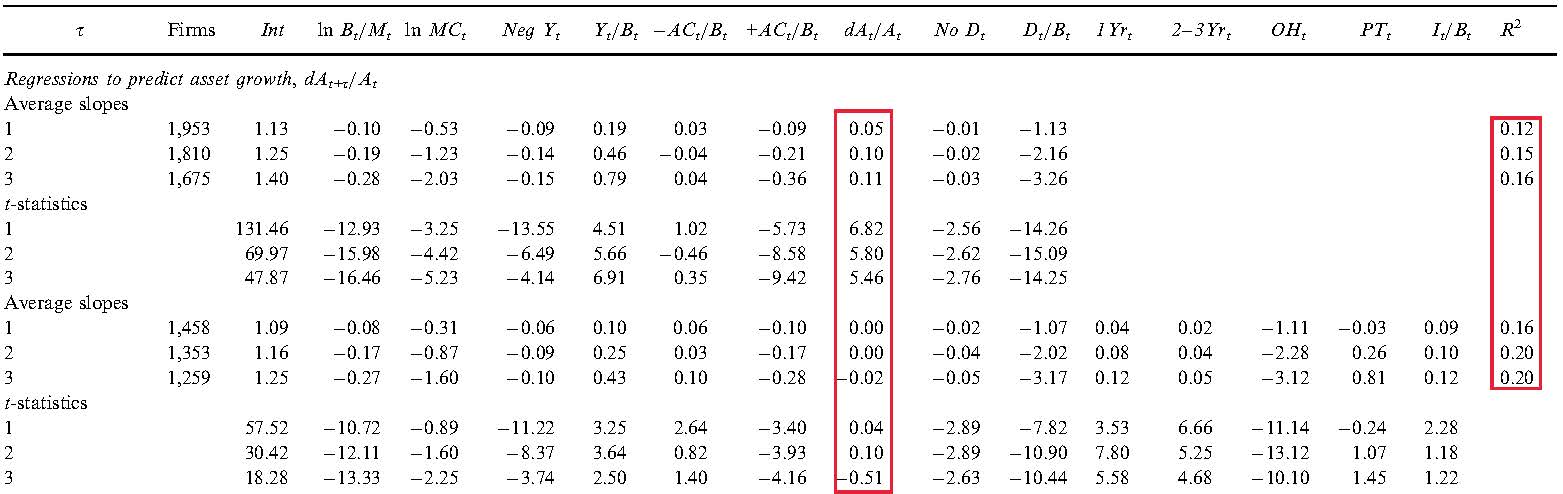
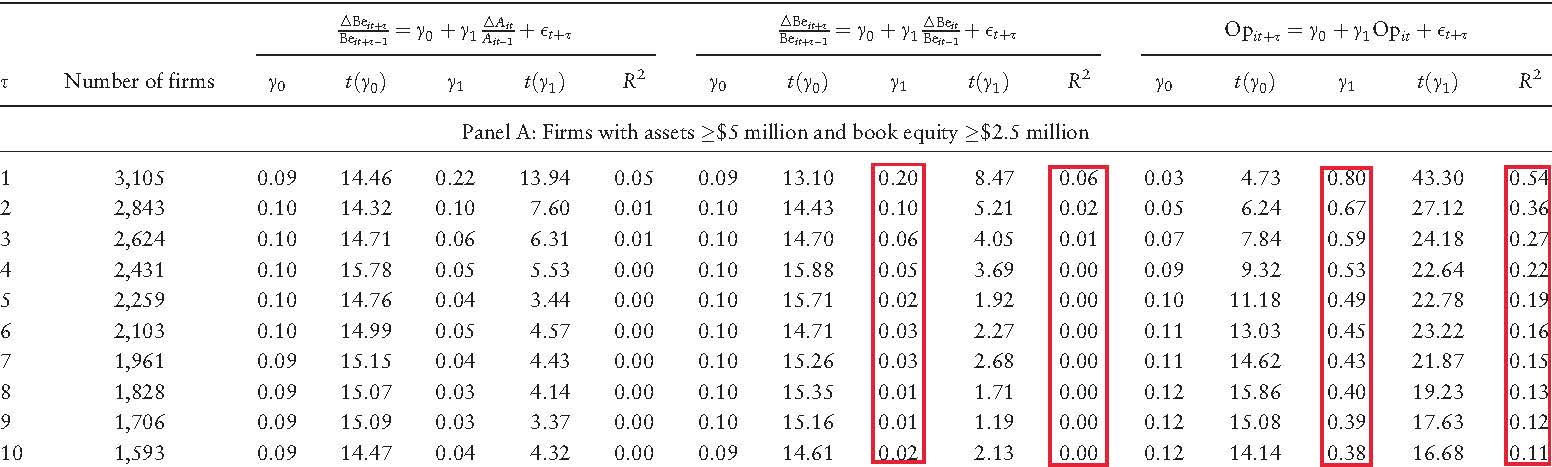


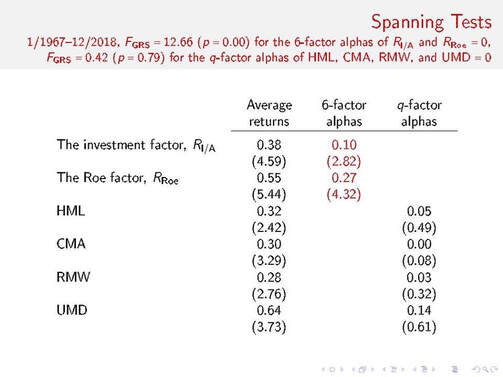
 RSS Feed
RSS Feed